Las fracciones son una parte fundamental de las matemáticas y se usan en una variedad de situaciones en nuestra vida diaria. Una fracción representa una parte de un todo, dividido en partes iguales. Por ejemplo, una pizza dividida en 8 rebanadas, cada rebanada sería 1/8 de la pizza. Nos enfocaremos en las fracciones equivalentes y cómo obtenerlas a partir de una fracción dada.

Te mostraremos un proceso sencillo para obtener fracciones equivalentes a una fracción dada. Aprenderemos a simplificar fracciones, es decir, reducir una fracción a su forma más simple y también a ampliar fracciones, es decir, multiplicar tanto el numerador como el denominador por el mismo número. Veremos ejemplos prácticos y explicaremos paso a paso cómo puedes obtener fracciones equivalentes a 3/4. ¡Sigue leyendo para aprender más!

Entendiendo las fracciones equivalentes

Las fracciones equivalentes son aquellas que representan la misma cantidad o valor, pero tienen diferentes numeradores y denominadores. Es decir, aunque se vean diferentes, en realidad representan lo mismo. Para entender mejor las fracciones equivalentes, es necesario comprender algunos conceptos básicos.

Numerador y denominador

En una fracción, el numerador representa la cantidad de partes que se tienen o se consideran, mientras que el denominador indica en cuántas partes se divide el todo. Por ejemplo, en la fracción 2/3, el numerador es 2 y el denominador es 3. Esto significa que se tienen dos partes de un todo dividido en tres partes iguales.

Multiplicar o dividir por el mismo número

Una forma de obtener fracciones equivalentes es multiplicando o dividiendo tanto el numerador como el denominador por el mismo número. Esto no altera el valor de la fracción, ya que se está multiplicando o dividiendo tanto la parte como el todo por el mismo número.

Por ejemplo, si queremos encontrar una fracción equivalente a 2/3, podemos multiplicar tanto el numerador como el denominador por 2:

• 2 * 2 = 4
• 3 * 2 = 6

Entonces, la fracción 2/3 es equivalente a 4/6. Ambas representan la misma cantidad o valor, pero tienen diferentes numeradores y denominadores.

Simplificar una fracción

Por otro lado, también es posible simplificar una fracción sin alterar su valor. Esto se logra dividiendo tanto el numerador como el denominador por el mismo número que sea divisor común de ambos.

Por ejemplo, la fracción 4/6 se puede simplificar dividiendo tanto el numerador como el denominador por 2:

• 4 ÷ 2 = 2
• 6 ÷ 2 = 3

Entonces, la fracción 4/6 se simplifica a 2/3, que es una fracción equivalente.

Uso de fracciones equivalentes

Las fracciones equivalentes son útiles en diversas situaciones, como por ejemplo, al comparar cantidades o al realizar operaciones matemáticas. Al tener diferentes representaciones de una misma cantidad, es posible utilizar la fracción que resulte más conveniente en cada caso.

Además, al trabajar con fracciones equivalentes, se pueden realizar cálculos más sencillos, ya que es posible utilizar fracciones con numeradores y denominadores más pequeños.

Las fracciones equivalentes son aquellas que representan la misma cantidad o valor, pero tienen diferentes numeradores y denominadores. Se pueden obtener multiplicando o dividiendo tanto el numerador como el denominador por el mismo número. También es posible simplificar una fracción dividiendo tanto el numerador como el denominador por el mismo número. El uso de fracciones equivalentes facilita la comparación de cantidades y la realización de operaciones matemáticas.

¿Qué es una fracción y cómo se representa?

Una fracción es un concepto matemático que representa una cantidad que es parte de un todo. Está compuesta por dos números, separados por una línea horizontal llamada barra de fracción. El número de arriba se llama numerador y el de abajo se llama denominador.

Representación de una fracción

Para representar una fracción, se utiliza la notación numérica en forma de "a/b", donde "a" representa el numerador y "b" representa el denominador. Por ejemplo, la fracción 3/4 significa que se están tomando 3 partes de un total de 4 partes.

Tipos de fracciones

Las fracciones pueden clasificarse en diferentes tipos, dependiendo de las características de su numerador y denominador:

1. Fracciones propias: aquellas en las que el numerador es menor que el denominador, es decir, la cantidad que representa es menor a la unidad.
2. Fracciones impropias: aquellas en las que el numerador es mayor o igual que el denominador, es decir, la cantidad que representa es igual o mayor a la unidad.
3. Fracciones mixtas: aquellas que combinan un número entero con una fracción propia, por ejemplo, 2 1/2.

Operaciones con fracciones

Existen diferentes operaciones que se pueden realizar con fracciones, entre ellas:

• Suma y resta: para sumar o restar fracciones, se deben tener el mismo denominador. Una vez que se tienen los mismos denominadores, se suman o restan los numeradores y se deja el denominador común.
• Multiplicación: para multiplicar fracciones, se multiplican los numeradores y los denominadores entre sí.
• División: para dividir fracciones, se multiplica la fracción dividendo por el inverso multiplicativo de la fracción divisor.

Uso de fracciones en la vida cotidiana

Las fracciones se utilizan en muchas situaciones cotidianas, como:

• Mediciones: por ejemplo, cuando se utiliza una receta de cocina y se necesita medir una cantidad de un ingrediente que no es una cantidad entera.
• Porcentajes: los porcentajes se pueden representar como fracciones, por ejemplo, el 50% se puede expresar como 1/2.
• División equitativa: cuando se quiere dividir algo entre varias personas de manera justa, como repartir una pizza.

Las fracciones son una herramienta matemática fundamental que nos permite representar partes de un todo y realizar operaciones con ellas. Su uso es amplio y se aplica en diversas situaciones de la vida cotidiana.

¿Cómo se determina si dos fracciones son equivalentes?

Para determinar si dos fracciones son equivalentes, se deben comparar sus valores. Dos fracciones son equivalentes si representan la misma cantidad. En otras palabras, si dos fracciones tienen el mismo valor decimal, entonces son equivalentes.

Existen diferentes métodos para determinar si dos fracciones son equivalentes. A continuación, se presentan algunos de los más comunes:

Método 1: Simplificar las fracciones
Una forma de determinar si dos fracciones son equivalentes es simplificarlas a su forma más reducida. Si dos fracciones simplificadas son iguales, entonces las fracciones originales también son equivalentes.

Para simplificar una fracción, se deben encontrar los factores primos del numerador y denominador y dividirlos entre el máximo común divisor. El máximo común divisor es el número más grande que divide exactamente al numerador y denominador.

Método 2: Multiplicar o dividir por el mismo número
Otra forma de determinar si dos fracciones son equivalentes es multiplicar o dividir el numerador y denominador de una fracción por el mismo número. Si las fracciones resultantes son iguales, entonces las fracciones originales también son equivalentes.

Por ejemplo, si tenemos las fracciones 2/3 y 4/6, podemos multiplicar el numerador y denominador de la primera fracción por 2, obteniendo 4/6. Como ambas fracciones son iguales, podemos concluir que son equivalentes.

Método 3: Comparar los valores decimales
Una forma rápida de determinar si dos fracciones son equivalentes es convertirlas en valores decimales y compararlos. Si las fracciones tienen el mismo valor decimal, entonces son equivalentes.

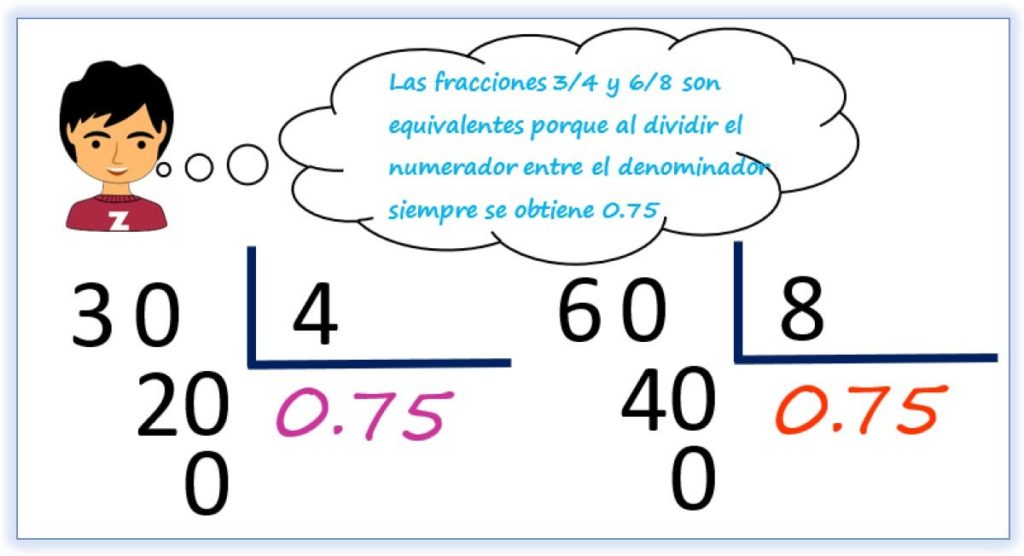
Para convertir una fracción en un valor decimal, se debe dividir el numerador entre el denominador. Por ejemplo, si tenemos la fracción 3/4, se realizaría la operación 3 ÷ 4 = 0.75. Si tenemos la fracción 6/8, se realizaría la operación 6 ÷ 8 = 0.75. Como ambos valores decimales son iguales, podemos concluir que las fracciones son equivalentes.

Estos son solo algunos métodos para determinar si dos fracciones son equivalentes. Es importante recordar que dos fracciones son equivalentes si representan la misma cantidad, independientemente de su forma.

Pasos para obtener fracciones equivalentes a 3/4

Si deseas obtener fracciones equivalentes a 3/4, puedes seguir los siguientes pasos:

Paso 1: Encuentra un denominador común

El primer paso para obtener fracciones equivalentes a 3/4 es encontrar un denominador común. Esto significa que necesitamos encontrar un número que sea divisible tanto por 4 como por el denominador deseado.

Paso 2: Multiplica el numerador y el denominador por el mismo número

Una vez que encuentres el denominador común, deberás multiplicar tanto el numerador como el denominador de la fracción original (3/4) por el mismo número. Esto dará lugar a una fracción equivalente.

Paso 3: Simplifica si es necesario

Finalmente, si la fracción equivalente resultante no está simplificada, puedes simplificarla dividiendo tanto el numerador como el denominador por su máximo común divisor. Esto te dará la fracción equivalente en su forma más simple.

Ahora que conoces los pasos para obtener fracciones equivalentes a 3/4, puedes aplicarlos para encontrar otras fracciones equivalentes a cualquier número dado.

Método de multiplicación para obtener fracciones equivalentes

Una forma común de obtener fracciones equivalentes es utilizando el método de multiplicación. Este método consiste en multiplicar tanto el numerador como el denominador de una fracción por el mismo número, lo que resulta en una fracción equivalente pero con valores diferentes.

Para utilizar este método, primero se elige un número por el cual se va a multiplicar la fracción. Este número puede ser cualquier número entero, siempre y cuando no sea cero. Luego, se multiplica tanto el numerador como el denominador de la fracción por este número.

Por ejemplo, si tenemos la fracción 2/3 y queremos obtener una fracción equivalente, podemos multiplicar tanto el numerador (2) como el denominador (3) por algún número. Si elegimos multiplicarlos por 2, obtendremos la fracción equivalente 4/6. Si elegimos multiplicarlos por 3, obtendremos la fracción equivalente 6/9. Y así sucesivamente.

Es importante destacar que al multiplicar una fracción por un número, su valor no se altera, ya que estamos multiplicando tanto el numerador como el denominador por el mismo número. Lo que estamos haciendo es expresar la misma cantidad en formas diferentes, es decir, en diferentes fracciones equivalentes.

Este método es útil cuando queremos simplificar una fracción, ya que nos permite encontrar una fracción equivalente en la que el numerador y el denominador sean lo más pequeños posibles. Por ejemplo, si tenemos la fracción 12/16 y queremos simplificarla, podemos multiplicar tanto el numerador como el denominador por 0.5, lo que nos dará la fracción equivalente 6/8. Luego, podemos seguir simplificándola multiplicando ambos números por 0.75, obteniendo finalmente la fracción simplificada 3/4.

Método de división para obtener fracciones equivalentes

El método de división es una forma sencilla y efectiva de obtener fracciones equivalentes. Se basa en la propiedad fundamental de las fracciones, que establece que si se multiplica o divide tanto el numerador como el denominador de una fracción por el mismo número, se obtiene una fracción equivalente.

El procedimiento es el siguiente:

Paso 1: Elije una fracción inicial

Para comenzar, elige una fracción con la que deseas trabajar. Puede ser cualquier fracción, por ejemplo, 2/3.

Paso 2: Elije un número para dividir la fracción

Ahora, selecciona un número por el cual deseas dividir la fracción. Este número puede ser cualquier valor, siempre y cuando no sea cero.

Paso 3: Divide el numerador y el denominador

Divide el numerador y el denominador de la fracción inicial por el número seleccionado en el paso anterior. Por ejemplo, si elegiste dividir la fracción 2/3 por 2, deberás dividir 2 entre 2 y 3 entre 2.

Paso 4: Simplifica la fracción, si es necesario

Si el resultado de la división anterior no es una fracción irreducible, es decir, si el numerador y el denominador tienen factores comunes, simplifica la fracción dividiendo ambos términos por su máximo común divisor.

Paso 5: Obtén una fracción equivalente

El resultado de la simplificación, si es necesario, será una fracción equivalente a la fracción inicial que elegiste. ¡Y eso es todo! Has obtenido una fracción equivalente utilizando el método de división.

Este método puede repetirse tantas veces como se desee para obtener más fracciones equivalentes. Simplemente elige una nueva fracción inicial y repite los pasos anteriores.

Ejemplos prácticos para entender el proceso

Ahora vamos a ver algunos ejemplos prácticos para entender mejor el proceso de codificación en HTML.

Ejemplo 1: Listas

En este ejemplo, vamos a crear una lista no ordenada con tres elementos:

• Elemento 1
• Elemento 2
• Elemento 3

Para crear esta lista, utilizamos la etiqueta <ul> para iniciar la lista y la etiqueta <li> para cada elemento de la lista. Al cerrar las etiquetas, obtenemos la lista no ordenada con los elementos enumerados.

Ejemplo 2: Encabezados

En este ejemplo, vamos a utilizar los encabezados HTML para estructurar un texto:

Encabezado 1

Este es un párrafo de texto.

Encabezado 2

Este es otro párrafo de texto.

En este caso, utilizamos las etiquetas <h1> y <h2> para crear los encabezados. Cada encabezado tiene un tamaño y nivel diferente, siendo <h1> el más grande y <h6> el más pequeño.

Ejemplo 3: Listas ordenadas

En este último ejemplo, vamos a crear una lista ordenada con cinco elementos:

1. Elemento 1
2. Elemento 2
3. Elemento 3
4. Elemento 4
5. Elemento 5

Para crear esta lista, utilizamos la etiqueta <ol> para iniciar la lista y la etiqueta <li> para cada elemento de la lista. Al cerrar las etiquetas, obtenemos la lista ordenada con los elementos numerados.

Consejos adicionales para trabajar con fracciones equivalentes

Trabajar con fracciones equivalentes puede resultar complicado al principio, pero con práctica y algunos consejos adicionales, podrás dominar este concepto matemático de manera más fácil. Aquí tienes algunos consejos que pueden ser útiles:

1. Simplificar las fracciones

Antes de buscar fracciones equivalentes, es recomendable simplificar las fracciones originales lo más que se pueda. Esto hará que sea más fácil encontrar otras fracciones equivalentes y reducirá la posibilidad de cometer errores.

2. Utilizar el método de multiplicación/división

Una forma común de encontrar fracciones equivalentes es utilizando el método de multiplicación/división. Si tienes una fracción y quieres encontrar una fracción equivalente, puedes multiplicar o dividir tanto el numerador como el denominador por el mismo número. Esto no afectará el valor de la fracción, pero te dará una forma diferente de representarla.

3. Utilizar el método de suma/resta

Otra forma de encontrar fracciones equivalentes es utilizando el método de suma/resta. Puedes sumar o restar el mismo número al numerador y al denominador de una fracción para obtener una fracción equivalente. Asegúrate de que el número que utilices para sumar o restar sea un múltiplo común del numerador y del denominador.

4. Utilizar el método de factores primos

Otro método para encontrar fracciones equivalentes es utilizar el método de factores primos. Descompón tanto el numerador como el denominador en factores primos y luego simplifica la fracción dividiendo los factores primos comunes.

5. Comprobar las fracciones equivalentes

Una vez que encuentres una fracción equivalente, compruébala calculando su valor y comparándola con la fracción original. Si ambas fracciones tienen el mismo valor, entonces son equivalentes.

Siguiendo estos consejos y practicando regularmente, podrás adquirir más fluidez en el manejo de fracciones equivalentes y mejorar tus habilidades matemáticas.

Importancia de las fracciones equivalentes en la vida diaria

Las fracciones equivalentes son una herramienta matemática fundamental que tiene una relevancia significativa en nuestra vida diaria. Estas fracciones nos permiten representar y comparar partes de un todo, lo cual es esencial en muchas situaciones cotidianas.

Distribución de alimentos

Un ejemplo claro de la importancia de las fracciones equivalentes se encuentra en la distribución de alimentos. En muchos casos, los alimentos se dividen en fracciones para poder repartirlos de manera equitativa entre un grupo de personas. Por ejemplo, si se tiene un pastel para 8 personas y se quiere asegurar que cada una reciba una cantidad igual de pastel, es necesario utilizar fracciones equivalentes para dividir el pastel en porciones iguales.

• En este caso, se puede utilizar una fracción equivalente para dividir el pastel en 8 porciones iguales:
• 1/8 del pastel representa una porción para cada persona.
• 2/8 del pastel representan dos porciones para cada persona.
• Y así sucesivamente, hasta alcanzar las 8 porciones equitativas.

Medidas de tiempo

Otro ejemplo donde las fracciones equivalentes son fundamentales es en la medición del tiempo. En nuestro día a día, utilizamos fracciones equivalentes para expresar el tiempo transcurrido en diferentes unidades de medida.

• Por ejemplo, si queremos expresar que hemos pasado la mitad del día, utilizamos la fracción equivalente 1/2 para representar ese momento.
• Si queremos expresar que han pasado 15 minutos de la hora actual, utilizamos la fracción equivalente 1/4, ya que 15 minutos es la cuarta parte de una hora.

Repartición de gastos

En situaciones donde varias personas deben dividir los gastos de un evento o una compra, las fracciones equivalentes son necesarias para lograr una distribución justa. Por ejemplo, si se van a repartir los gastos de un viaje entre 4 personas, se utilizan fracciones equivalentes para dividir el total en partes iguales.

• Si el total del viaje es de $400 y se quiere repartir equitativamente entre las 4 personas, se utiliza la fracción equivalente 1/4 para determinar cuánto debe pagar cada una.
• Cada persona deberá pagar 1/4 de los $400, es decir, $100.

Las fracciones equivalentes son una herramienta matemática que nos permite representar y comparar partes de un todo en situaciones cotidianas. Desde la distribución de alimentos, hasta la medición del tiempo y la repartición de gastos, las fracciones equivalentes juegan un papel fundamental en nuestra vida diaria.

Preguntas frecuentes

1. ¿Qué es una fracción equivalente?

Una fracción equivalente es aquella que representa la misma cantidad, pero con diferentes números en el numerador y el denominador.

2. ¿Cómo puedo obtener fracciones equivalentes a 3/4?

Puedes obtener fracciones equivalentes multiplicando o dividiendo tanto el numerador como el denominador de la fracción original por el mismo número.

3. ¿Puedo simplificar una fracción equivalente a 3/4?

Sí, puedes simplificar una fracción equivalente a 3/4 dividiendo tanto el numerador como el denominador por un número que sea divisor común de ambos.

4. ¿Puedo obtener una fracción equivalente a 3/4 que sea mayor o menor?

Sí, puedes obtener una fracción equivalente a 3/4 que sea mayor o menor multiplicando o dividiendo tanto el numerador como el denominador por un número mayor que 1 o menor que 1, respectivamente.

5. ¿Cuántas fracciones equivalentes puedo obtener a partir de 3/4?

Existen infinitas fracciones equivalentes a partir de 3/4, ya que se pueden multiplicar o dividir por cualquier número diferente de cero.