Descubre cómo se pueden formar triángulos equiláteros con un ángulo recto puede cambiar tu perspectiva matemática

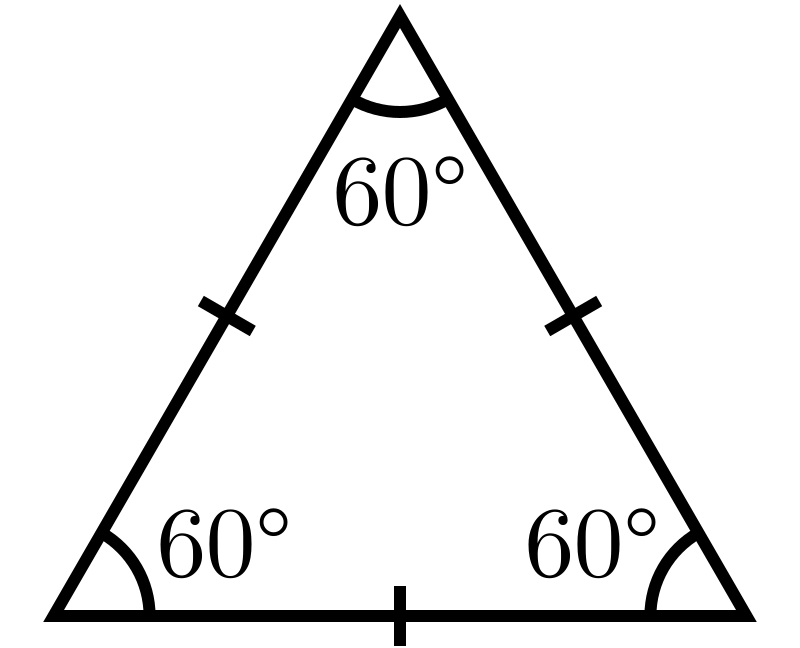
Los triángulos equiláteros son figuras geométricas fascinantes debido a su simetría y propiedades únicas. Estos triángulos tienen tres lados iguales y tres ángulos iguales de 60 grados cada uno. Su estructura equilibrada los convierte en elementos importantes en diversas áreas de las matemáticas y la física.

Exploraremos cómo se pueden formar triángulos equiláteros con un ángulo recto. Veremos diferentes métodos y demostraciones matemáticas para lograrlo. También discutiremos las implicaciones y aplicaciones de estos triángulos en diversos campos, desde la construcción hasta la ingeniería. Prepárate para ampliar tu perspectiva matemática y descubrir nuevas formas de pensar sobre los triángulos equiláteros.

Introducción a los triángulos equiláteros y su importancia en la geometría

Los triángulos equiláteros son una figura geométrica importante en el campo de la geometría. Son un tipo de triángulo en el cual todos sus lados son iguales y, por lo tanto, todos sus ángulos también son iguales. Esto significa que cada uno de los ángulos internos del triángulo equilátero mide exactamente 60 grados.

Esta característica hace que los triángulos equiláteros sean muy especiales, ya que son la única clase de triángulos en los que todos los ángulos son iguales y tienen una medida de 60 grados. Además, todos los triángulos equiláteros son congruentes entre sí, lo que significa que tienen la misma forma y tamaño.

En la geometría, los triángulos equiláteros se estudian por sus propiedades únicas y sus aplicaciones en diferentes contextos. Algunas de las propiedades más importantes de los triángulos equiláteros incluyen:

• Todos los lados son iguales.
• Todos los ángulos internos miden 60 grados.
• Los triángulos equiláteros son simétricos respecto a sus ejes de simetría, lo que significa que se pueden dividir en dos partes iguales si se traza una línea recta a través de su centro.
• El centroide, el circuncentro, el incentro y el ortocentro de un triángulo equilátero coinciden en un solo punto.
• Los triángulos equiláteros son utilizados en la construcción de diferentes figuras geométricas, como hexágonos regulares y tetraedros regulares.

Además de sus propiedades y aplicaciones en la geometría, los triángulos equiláteros también tienen un significado simbólico en diferentes culturas y religiones alrededor del mundo. Por ejemplo, en la geometría sagrada, el triángulo equilátero se considera un símbolo de perfección y equilibrio.

Los triángulos equiláteros son una figura geométrica especial y significativa debido a sus propiedades únicas y sus aplicaciones en la geometría. Su forma perfectamente equilibrada y simétrica los convierte en una figura de estudio y admiración dentro de este campo. Además, su significado simbólico trasciende a lo geométrico y se encuentra presente en diferentes culturas alrededor del mundo.

El concepto de ángulo recto y su relación con los triángulos equiláteros

El concepto de ángulo recto es fundamental en geometría y juega un papel importante en la resolución de problemas geométricos. Un ángulo recto es aquel que mide exactamente 90 grados, es decir, es la mitad de un ángulo llano y la cuarta parte de un ángulo completo.

En la geometría euclidiana, un triángulo equilátero es aquel que tiene sus tres lados iguales. Es un caso especial de triángulo, ya que todos sus ángulos internos miden 60 grados. Además, cada ángulo interno de un triángulo equilátero es también un ángulo recto, lo que lo convierte en un triángulo excepcional.

La relación entre el concepto de ángulo recto y los triángulos equiláteros se basa en el hecho de que, al ser un triángulo equilátero, sus ángulos internos miden 60 grados cada uno. Como se mencionó anteriormente, un ángulo recto mide 90 grados, por lo que los ángulos internos de un triángulo equilátero son más pequeños que un ángulo recto.

Esta relación puede ser útil para la resolución de problemas geométricos, ya que permite establecer una comparación entre los ángulos rectos y los ángulos internos del triángulo equilátero. Además, el triángulo equilátero tiene propiedades interesantes que pueden aplicarse en la construcción de figuras y en la demostración de teoremas geométricos.

El concepto de ángulo recto es fundamental en geometría y se relaciona con los triángulos equiláteros debido a que sus ángulos internos son más pequeños que un ángulo recto. Esta relación puede ser utilizada en la resolución de problemas geométricos y en la demostración de teoremas.

Cómo formar triángulos equiláteros con un ángulo recto a partir de construcciones geométricas

En la construcción geométrica de triángulos, uno de los casos más comunes es el de los triángulos equiláteros. Estos triángulos poseen tres lados iguales y tres ángulos iguales de 60 grados cada uno.

Sin embargo, ¿es posible construir un triángulo equilátero que además tenga un ángulo recto? La respuesta es sí, y en este artículo te mostraré cómo lograrlo a través de diversas construcciones geométricas.

Construcción 1: Utilizando un compás y una regla

1. Dibuja un segmento de línea recta AB utilizando una regla.
2. Coloca la punta del compás en el punto A y ajusta su abertura para que sea igual a la longitud del segmento AB.
3. Realiza un arco desde el punto B hasta cortar la línea recta AB en el punto C.
4. Coloca la punta del compás en el punto C y ajusta su abertura para que sea igual a la longitud del segmento AC.
5. Realiza otro arco desde el punto A hasta cortar la línea recta AB en el punto D.
6. La intersección de los dos arcos en el punto D es el vértice del triángulo equilátero con ángulo recto.
7. Conecta los puntos A, B y D para formar el triángulo equilátero con ángulo recto.

Construcción 2: Utilizando una cuerda y clavos

1. Clava tres clavos en forma de triángulo en una tablilla, de manera que formen un triángulo equilátero.
2. Pasa una cuerda alrededor de los tres clavos, de forma que quede bien tensa.
3. Coloca un lápiz en el punto donde se cruzan la cuerda y la tablilla.
4. Gira el lápiz alrededor de este punto, manteniendo la cuerda tensa.
5. El lápiz trazará un arco en la tablilla, generando un triángulo equilátero con ángulo recto.

Estas dos construcciones te permiten formar triángulos equiláteros con un ángulo recto utilizando herramientas básicas de geometría. Recuerda que la precisión en las mediciones y el trazo de líneas es fundamental para obtener resultados óptimos.

Ejemplos prácticos de triángulos equiláteros con un ángulo recto y su utilidad en problemas matemáticos

Los triángulos equiláteros con un ángulo recto son aquellos triángulos que cumplen con dos características importantes: todos sus lados son iguales y uno de sus ángulos internos mide 90 grados. Este tipo de triángulos son muy interesantes y útiles en diversas áreas de las matemáticas, ya que nos permiten resolver problemas y plantear situaciones de forma más sencilla y eficiente.

¿Cómo identificar un triángulo equilátero con un ángulo recto?

Para identificar un triángulo equilátero con un ángulo recto, debemos verificar dos condiciones:

• Todos los lados del triángulo deben tener la misma longitud. Esto implica que si conocemos la medida de uno de los lados, podemos determinar la medida de los otros dos lados.
• Uno de los ángulos internos del triángulo debe medir 90 grados. Esto significa que uno de los lados del triángulo será perpendicular al otro, formando un ángulo recto.

Si ambas condiciones se cumplen, entonces podemos afirmar que estamos frente a un triángulo equilátero con un ángulo recto.

Utilidad en problemas matemáticos

Los triángulos equiláteros con un ángulo recto pueden resultar muy útiles en la resolución de problemas matemáticos. Algunas de sus aplicaciones más comunes son:

1. Cálculo de áreas: Al conocer la longitud de uno de los lados del triángulo equilátero y tener un ángulo recto, podemos calcular fácilmente el área del triángulo utilizando la fórmula del área de un triángulo rectángulo.
2. Resolución de problemas de geometría: Los triángulos equiláteros con un ángulo recto pueden ser utilizados para resolver problemas de geometría que involucren ángulos, lados y áreas.
3. Problemas de trigonometría: Al tener un ángulo recto y conocer la longitud de los lados del triángulo equilátero, podemos aplicar fórmulas trigonométricas para resolver problemas relacionados con razones trigonométricas como el seno, coseno y tangente.

Los triángulos equiláteros con un ángulo recto son una herramienta matemática muy útil y versátil. Su propiedad de tener lados iguales y un ángulo recto nos permite resolver problemas de geometría y trigonometría de manera más sencilla. Además, son fundamentales en el cálculo de áreas de triángulos rectángulos. Conocer y comprender estas propiedades nos ayudará a resolver problemas matemáticos de manera más eficiente.

La importancia de la simetría en los triángulos equiláteros con un ángulo recto

En la geometría, la simetría es un concepto ampliamente estudiado y utilizado. Se refiere a la propiedad de una figura o un objeto de mantener su forma o apariencia a medida que se realiza una transformación. Uno de los casos más interesantes es la simetría en los triángulos equiláteros con un ángulo recto.

Un triángulo equilátero es aquel que tiene sus tres lados iguales y sus tres ángulos internos de 60 grados cada uno. Cuando se le añade un ángulo recto, es decir, un ángulo de 90 grados, se produce una figura aún más especial y simétrica.

Simetría respecto a la altura

Una de las formas de simetría que podemos encontrar en estos triángulos es la simetría respecto a la altura. La altura de un triángulo es la línea perpendicular que se traza desde un vértice hasta el lado opuesto. En un triángulo equilátero con un ángulo recto, la altura divide al triángulo en dos triángulos rectángulos isósceles, es decir, con un ángulo recto y dos lados iguales.

Si trazamos la altura desde cada vértice y unimos los puntos de intersección, obtendremos un punto de simetría en el centro del triángulo. Esto significa que si giramos el triángulo 180 grados sobre este punto, obtendremos una figura idéntica. Esta simetría nos permite reconocer patrones y propiedades geométricas de manera más fácil.

Simetría respecto a los ejes de simetría

Otra forma de simetría que se puede apreciar en estos triángulos es la simetría respecto a los ejes de simetría. Los ejes de simetría son las líneas que dividen a una figura en dos partes iguales y simétricas. En un triángulo equilátero con un ángulo recto, encontramos tres ejes de simetría: las medianas y las bisectrices.

Las medianas son las líneas que unen cada vértice con el punto medio del lado opuesto. En un triángulo equilátero con un ángulo recto, las medianas también actúan como ejes de simetría. Esto significa que si reflejamos el triángulo sobre cada una de las medianas, obtendremos una figura idéntica.

Las bisectrices son las líneas que dividen a los ángulos internos en dos partes iguales. En un triángulo equilátero con un ángulo recto, las bisectrices también actúan como ejes de simetría. Esto significa que si reflejamos el triángulo sobre cada una de las bisectrices, obtendremos una figura idéntica.

La simetría en los triángulos equiláteros con un ángulo recto es una propiedad que nos permite reconocer patrones, encontrar propiedades geométricas y facilitar los cálculos. La simetría respecto a la altura y los ejes de simetría nos ayudan a entender mejor la estructura y las características de estos triángulos.

Aplicaciones de los triángulos equiláteros con un ángulo recto en la vida cotidiana y en otras disciplinas

Los triángulos equiláteros con un ángulo recto tienen diversas aplicaciones tanto en la vida cotidiana como en otras disciplinas. A continuación, se presentan algunas de estas aplicaciones:

En la arquitectura y la construcción

Los triángulos equiláteros con un ángulo recto son utilizados en la arquitectura y la construcción para diseñar estructuras estables y equilibradas. Estos triángulos permiten distribuir de manera uniforme las cargas y resistir fuerzas externas, lo que contribuye a la resistencia y durabilidad de las construcciones.

En la geometría y la trigonometría

Los triángulos equiláteros con un ángulo recto son utilizados en la geometría y la trigonometría para realizar cálculos y resolver problemas. Estos triángulos son especialmente útiles para determinar relaciones entre los lados y los ángulos de un triángulo, así como para aplicar teoremas y fórmulas geométricas.

En la electrónica y la tecnología

Los triángulos equiláteros con un ángulo recto también son utilizados en la electrónica y la tecnología. Estos triángulos se utilizan en el diseño de circuitos electrónicos y en la colocación de componentes, ya que permiten minimizar la interferencia y optimizar el rendimiento de los dispositivos electrónicos.

En la astronomía y la navegación

Los triángulos equiláteros con un ángulo recto son utilizados en la astronomía y la navegación para determinar la posición y la distancia de objetos celestes y terrestres. Estos triángulos son utilizados en combinación con instrumentos como sextantes y teodolitos para realizar mediciones y cálculos precisos.

En el arte y el diseño

Los triángulos equiláteros con un ángulo recto también son utilizados en el arte y el diseño para crear composiciones equilibradas y armoniosas. Estos triángulos se utilizan en el diseño gráfico, la pintura y la escultura, entre otras disciplinas, para crear estructuras visuales atractivas y estéticamente equilibradas.

Los triángulos equiláteros con un ángulo recto tienen múltiples aplicaciones en la vida cotidiana y en otras disciplinas. Su forma simétrica y sus propiedades geométricas los convierten en herramientas útiles para resolver problemas, diseñar estructuras estables y crear composiciones artísticas y visuales atractivas.

Conclusiones sobre cómo la formación de triángulos equiláteros con un ángulo recto puede ampliar nuestra perspectiva matemática.

La formación de triángulos equiláteros con un ángulo recto es un tema fascinante en matemáticas que nos permite ampliar nuestra perspectiva y comprensión de los conceptos geométricos. A través de la exploración de esta figura geométrica especial, podemos descubrir propiedades únicas y establecer conexiones interesantes con otros conceptos matemáticos.

En primer lugar, hemos visto que un triángulo equilátero con un ángulo recto tiene una serie de propiedades notables. Por ejemplo, todos sus ángulos internos son de 60 grados, lo cual es una característica común de los triángulos equiláteros. Sin embargo, también tiene un ángulo recto, lo cual es menos común en este tipo de triángulo. Esta combinación única de ángulos nos permite explorar relaciones interesantes entre ellos y analizar las diferencias y similitudes con otros tipos de triángulos.

Además, también hemos observado que los triángulos equiláteros con un ángulo recto tienen una estructura simétrica que los hace especialmente atractivos desde un punto de vista estético y visual. La combinación de líneas rectas y ángulos precisos crea una figura geométrica equilibrada y armoniosa, lo cual puede ser apreciado tanto desde una perspectiva matemática como artística.

Otra conclusión importante que podemos extraer de este tema es la conexión entre los triángulos equiláteros con un ángulo recto y otros conceptos matemáticos. Por ejemplo, hemos visto cómo se puede utilizar esta figura geométrica para construir otros polígonos regulares, como hexágonos y octógonos. Esto nos muestra una relación interesante entre diferentes formas geométricas y nos permite generar nuevas ideas y conceptos a partir de ellas.

La formación de triángulos equiláteros con un ángulo recto es un tema que nos permite ampliar nuestra perspectiva matemática y explorar nuevas propiedades y conexiones entre diferentes conceptos geométricos. A través de la comprensión de esta figura geométrica especial, podemos enriquecer nuestro conocimiento matemático y apreciar la belleza de las formas y estructuras que nos rodean.

Preguntas frecuentes

1. ¿Qué es un triángulo equilátero?

Un triángulo equilátero es aquel que tiene todos sus lados y ángulos internos iguales.

2. ¿Qué es un ángulo recto?

Un ángulo recto es aquel cuya medida es de 90 grados.

3. ¿Es posible formar un triángulo equilátero con un ángulo recto?

No, no es posible formar un triángulo equilátero con un ángulo recto, ya que los ángulos internos de un triángulo equilátero miden 60 grados cada uno.

4. ¿De qué manera puedo formar un triángulo equilátero?

Para formar un triángulo equilátero, todos los lados deben tener la misma longitud. Puedes utilizar una regla o un compás para asegurarte de que los lados sean iguales.

5. ¿Cuáles son las propiedades de un triángulo equilátero?

Las propiedades de un triángulo equilátero son que sus tres lados son iguales, sus tres ángulos internos son iguales y miden 60 grados cada uno, y todos sus ángulos externos miden 120 grados.