Descubre cuál es más grande: ¿un décimo o un centésimo?

Las **matemáticas** son una disciplina fascinante que nos ayuda a comprender el mundo que nos rodea. En el ámbito de las **fracciones**, es común encontrar términos como **décimos** y **centésimos**, que representan partes de un número o una cantidad. Sin embargo, puede surgir la duda de cuál de estas dos fracciones es más grande. Exploraremos la diferencia entre un **décimo** y un **centésimo** y determinaremos cuál de ellos es mayor.

Exploraremos las propiedades de los **décimos** y los **centésimos**, analizando cómo se comparan entre sí y cuál de ellos es mayor. Veremos cómo se representan estas fracciones en la recta numérica y cómo podemos utilizar estrategias de comparación para determinar cuál es más grande. Además, explicaremos cómo se puede aplicar este conocimiento a situaciones cotidianas y cómo nos ayuda a comprender mejor conceptos matemáticos fundamentales. Sin más preámbulos, ¡comencemos nuestro viaje al mundo de las fracciones!

Significado y representación de un décimo y un centésimo

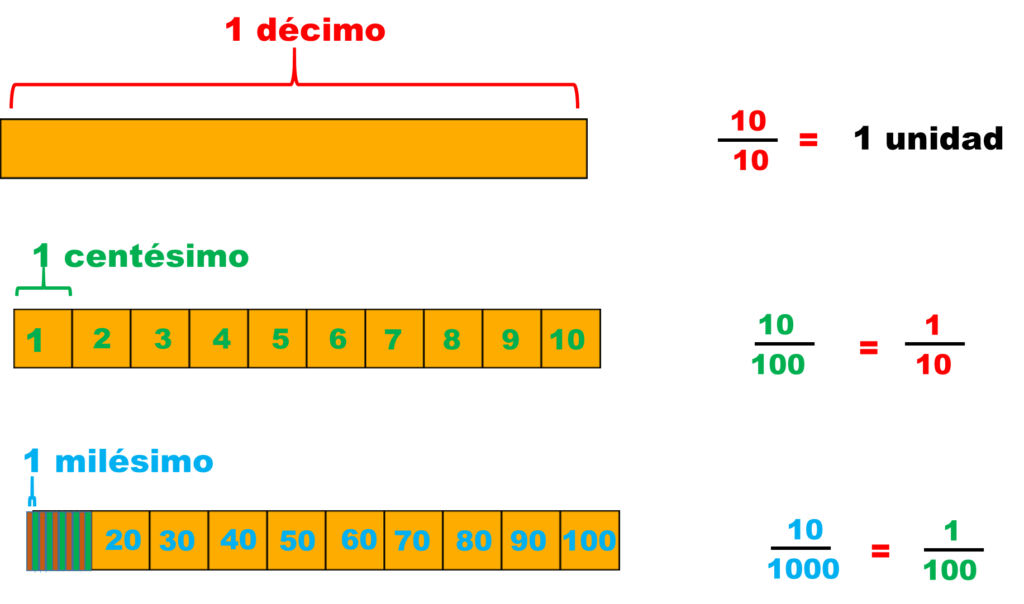
Un décimo es una fracción que representa una división igual en 10 partes iguales. Matemáticamente, se puede representar como 1/10. Un centésimo es otra fracción que representa una división igual en 100 partes iguales. Matemáticamente, se puede representar como 1/100.

Representación decimal

Los decimales también se pueden representar en forma decimal. Un décimo se representaría como 0.1 y un centésimo se representaría como 0.01. Estas representaciones decimales pueden tener un número ilimitado de decimales, dependiendo de la precisión requerida.

Representación porcentual

Además de la representación decimal, los décimos y los centésimos también se pueden representar en forma porcentual. Un décimo se puede expresar como el 10% de un número y un centésimo se puede expresar como el 1% de un número.

Uso en la lotería

En el contexto de la lotería, un décimo se refiere a una fracción de un billete de lotería completo. Los billetes de lotería suelen estar divididos en 10 décimos, lo que permite a varias personas compartir el costo del billete y participar en el sorteo. Cada décimo representa una décima parte del premio en caso de ganar. De manera similar, un centésimo se refiere a una fracción todavía más pequeña de un billete de lotería, donde cada centésimo representa una centésima parte del premio en caso de ganar.

Ejemplo

Supongamos que hay un premio de $1,000 en una lotería y compramos un décimo de un billete. En caso de ganar, recibiríamos $100, que es una décima parte del premio total. En otro escenario, si compramos un centésimo de un billete, recibiríamos $10 en caso de ganar, que es una centésima parte del premio total.

Un décimo y un centésimo son fracciones que representan divisiones iguales en 10 y 100 partes iguales, respectivamente. Se utilizan en varios contextos, incluida la representación decimal, la representación porcentual y en la lotería para dividir el premio entre varias personas.

Comparación entre un décimo y un centésimo en términos de tamaño

El tamaño de una fracción se determina por el denominador. En el caso de un décimo, el denominador es 10, lo que significa que la fracción representa una de las diez partes iguales en las que se divide un todo. Por otro lado, en el caso de un centésimo, el denominador es 100, lo que implica que la fracción representa una de las cien partes iguales en las que se divide un todo.

En términos de tamaño, un centésimo es más pequeño que un décimo. Esto se debe a que hay cien partes iguales en un todo cuando se divide en centésimos, mientras que hay solo diez partes iguales cuando se divide en décimos. Por lo tanto, cada centésimo es una fracción más pequeña que cada décimo.

Para ilustrar esto mejor, se puede utilizar una comparación visual. Imagina un pastel dividido en cien rebanadas iguales y otro pastel dividido en diez rebanadas iguales. Cada rebanada del primer pastel sería un centésimo, mientras que cada rebanada del segundo pastel sería un décimo. Es evidente que cada rebanada del primer pastel sería más pequeña que cada rebanada del segundo pastel debido a la mayor cantidad de rebanadas en el primero.

Un centésimo es más pequeño que un décimo en términos de tamaño. Esto se debe al hecho de que hay cien partes iguales en un todo cuando se divide en centésimos, mientras que solo hay diez partes iguales cuando se divide en décimos.

Ejemplos numéricos para ilustrar la diferencia entre un décimo y un centésimo

Para comprender mejor la diferencia entre un décimo y un centésimo, veamos algunos ejemplos numéricos:

Ejemplo 1:

Imaginemos que tenemos una pizza entera y la dividimos en 10 pedazos iguales. Cada pedazo sería un décimo de la pizza. Si queremos calcular cuántas porciones tendríamos si tomamos solo un décimo de la pizza, podemos utilizar una fracción:

• Porción de pizza = 1/10

Ejemplo 2:

Ahora, consideremos que tomamos uno de esos pedazos de pizza y lo dividimos en 10 partes más pequeñas. Cada una de estas partes sería un centésimo de la pizza. Si queremos calcular cuántas de estas porciones tendríamos si tomamos solo un centésimo de la pizza, nuevamente utilizamos una fracción:

• Porción de pizza = 1/100

Ejemplo 3:

Para visualizar mejor la diferencia, podemos comparar la cantidad de porciones obtenidas en el ejemplo 1 y el ejemplo 2. Si tomamos un décimo de la pizza, tendríamos 10 porciones, cada una representando un décimo de la pizza. Por otro lado, si tomamos un centésimo de la pizza, tendríamos 100 porciones, cada una representando un centésimo de la pizza.

Un décimo es una fracción que representa una de las 10 partes iguales en las que se divide un objeto completo, mientras que un centésimo es una fracción que representa una de las 100 partes iguales en las que se divide un objeto completo. La diferencia radica en la cantidad de divisiones y, por lo tanto, en la cantidad de porciones resultantes.

Importancia de comprender la diferencia entre fracciones decimales para el aprendizaje matemático

La comprensión de las fracciones decimales es fundamental para el aprendizaje matemático, ya que permite a los estudiantes desarrollar habilidades y conceptos matemáticos esenciales. Las fracciones decimales son una forma de representar números racionales y se caracterizan por tener un denominador de 10 o de una potencia de 10.

Estas fracciones decimales son especialmente importantes porque se utilizan ampliamente en la vida diaria, en situaciones como la manipulación de dinero, las mediciones y la comprensión de porcentajes. Por lo tanto, comprender las fracciones decimales es esencial para el éxito en la vida cotidiana y en muchas carreras profesionales.

Además, las fracciones decimales son la base de otros conceptos matemáticos más avanzados, como las operaciones con decimales, la conversión entre fracciones decimales y porcentajes, y la comparación de magnitudes. Por lo tanto, es crucial que los estudiantes dominen este tema antes de avanzar en su educación matemática.

Una forma efectiva de enseñar las fracciones decimales es a través de la manipulación de objetos tangibles, como fichas o monedas, para representar las fracciones en forma decimal. Esto permite a los estudiantes visualizar y manipular las fracciones decimales, lo que facilita su comprensión y su capacidad para realizar cálculos con ellas.

Además, es importante proporcionar a los estudiantes oportunidades para practicar la conversión entre fracciones decimales y porcentajes, ya que esto les dará una comprensión más profunda de cómo estas formas de representar números están relacionadas y cómo se pueden utilizar en diferentes situaciones.

Comprender las fracciones decimales es esencial para el aprendizaje matemático y para la vida cotidiana. Proporcionar a los estudiantes una base sólida en este tema les permitirá adquirir habilidades matemáticas avanzadas y tener éxito en su educación y en su futuro profesional.

Aplicaciones prácticas de los conceptos de décimo y centésimo en la vida cotidiana

Los conceptos de décimo y centésimo son fundamentales en nuestra vida cotidiana, ya que nos permiten expresar y entender medidas y cantidades más precisas. A continuación, veremos algunas aplicaciones prácticas de estos conceptos en diferentes situaciones:

1. Medición de tiempo

En nuestro día a día, utilizamos los conceptos de décimo y centésimo para medir el tiempo con mayor exactitud. Por ejemplo, podemos expresar una fracción de una hora en términos de décimos o centésimos. Esto es especialmente útil cuando realizamos actividades que requieren un tiempo específico, como cocinar o hacer ejercicio.

2. Medición de distancias

Al igual que en la medición de tiempo, los conceptos de décimo y centésimo nos permiten expresar distancias de forma más precisa. Por ejemplo, podemos utilizar décimos de kilómetro o centésimos de metro para medir la longitud de un campo de fútbol o la altura de un edificio.

3. Cálculo de porcentajes

Los porcentajes son una forma común de expresar proporciones o tasas. Los conceptos de décimo y centésimo nos ayudan a calcular y entender estos porcentajes de manera más precisa. Por ejemplo, si tenemos que calcular el 15% de una cantidad, podemos expresar ese porcentaje como 0.15, donde el 0 representa los décimos y el 15 representa los centésimos.

4. Mediciones de medicamentos

En el ámbito de la medicina, es crucial tener precisión al administrar medicamentos. Los conceptos de décimo y centésimo nos permiten expresar las dosis de forma exacta y evitar errores en la administración. Por ejemplo, una dosis de 0.2 ml o 0.05 mg puede ser requerida en ciertos tratamientos, y estos valores expresan los décimos y centésimos de mililitro o miligramo.

5. Cálculo de probabilidades

En el campo de las matemáticas y la estadística, los conceptos de décimo y centésimo son fundamentales en el cálculo de probabilidades. Por ejemplo, al calcular la probabilidad de que un evento ocurra, expresamos esa probabilidad como un número entre 0 y 1, donde 0 representa una probabilidad nula y 1 representa una probabilidad segura. Los valores entre 0 y 1, como 0.35 o 0.73, representan probabilidades en términos de décimos y centésimos.

Los conceptos de décimo y centésimo tienen muchas aplicaciones prácticas en nuestra vida cotidiana. Nos permiten medir el tiempo y las distancias con mayor precisión, calcular porcentajes de forma exacta, administrar medicamentos de manera segura y calcular probabilidades en diferentes situaciones. Por lo tanto, es importante comprender y utilizar estos conceptos para tener una mejor comprensión del mundo que nos rodea.

Cómo convertir entre un décimo y un centésimo

Para convertir entre un décimo y un centésimo, necesitamos conocer la relación entre estas dos fracciones y cómo se pueden expresar en forma decimal.

Convertir un décimo a un centésimo

Un décimo se puede representar como 0.1 en forma decimal. Para convertirlo en un centésimo, debemos mover el punto decimal dos lugares hacia la derecha. Esto nos dará 0.01, que es la representación decimal de un centésimo.

Convertir un centésimo a un décimo

Un centésimo se puede representar como 0.01 en forma decimal. Para convertirlo en un décimo, debemos mover el punto decimal dos lugares hacia la izquierda. Esto nos dará 0.1, que es la representación decimal de un décimo.

Ejemplo práctico

Imaginemos que tenemos una fracción que es equivalente a 0.01 en forma decimal y queremos convertirla en un décimo. Para hacer esto, multiplicamos el valor decimal por 10. Así:

• 0.01 * 10 = 0.1

Por lo tanto, 0.01 en forma decimal es equivalente a 0.1 en forma de décimo.

Del mismo modo, si tenemos una fracción que es equivalente a 0.1 en forma decimal y queremos convertirla en un centésimo, dividimos el valor decimal por 10. Así:

• 0.1 / 10 = 0.01

Por lo tanto, 0.1 en forma decimal es equivalente a 0.01 en forma de centésimo.

Ejercicios y problemas para practicar la comparación de fracciones decimales

La comparación de fracciones decimales es una habilidad matemática fundamental que los estudiantes deben dominar. Para practicar y mejorar esta habilidad, se pueden realizar una serie de ejercicios y problemas que permiten familiarizarse con el proceso de comparar fracciones decimales.

Ejercicios de comparación de fracciones decimales

1. Comparar las siguientes fracciones decimales y determinar cuál es mayor:

• 0.3 y 0.5
• 0.7 y 0.9
• 0.2 y 0.25

2. Ordenar las siguientes fracciones decimales de menor a mayor:

1. 0.65, 0.45, 0.75
2. 0.35, 0.42, 0.38
3. 0.15, 0.2, 0.18

3. Completar las siguientes comparaciones utilizando los símbolos "<", ">" o "=":

• 0.5 ___ 0.75
• 0.9 ___ 0.99
• 0.35 ___ 0.35

Problemas de comparación de fracciones decimales

1. Pedro tiene 0.6 de una pizza y Pablo tiene 0.75 de otra pizza. ¿Quién tiene más pizza?

2. En un concurso de salto largo, Luisa saltó 0.35 metros y María saltó 0.42 metros. ¿Quién saltó más lejos?

3. Jorge ahorró 0.25 dólares, mientras que Juan ahorró 0.18 dólares. ¿Quién ahorró más dinero?

Estos ejercicios y problemas ayudarán a los estudiantes a practicar y afianzar sus habilidades para comparar fracciones decimales. Es importante recordar que la práctica regular es clave para mejorar en matemáticas.

Errores comunes al comparar un décimo y un centésimo y cómo evitarlos

La comparación de números decimales es una tarea común en el desarrollo de software. Sin embargo, a menudo se cometen errores al comparar un número decimal de un decimal. Aquí te presentamos algunos de los errores más comunes y cómo evitarlos:

Error 1: Comparar directamente los valores

Uno de los errores más comunes es comparar directamente los valores decimales sin considerar la precisión. Por ejemplo, si se compara el valor "0.1" con "0.01" utilizando el operador de igualdad "==", es probable que se obtenga un resultado incorrecto ya que los números decimales pueden tener una representación imprecisa en un sistema binario.

Para evitar este error, es recomendable utilizar una función de comparación especializada que tenga en cuenta la precisión decimal. Por ejemplo, en JavaScript se puede utilizar la función "toFixed()" para redondear los números decimales antes de compararlos.

Error 2: Utilizar comparaciones estrictas

Otro error común es utilizar comparaciones estrictas, como el operador de igualdad estricta "===" o el operador de desigualdad estricta "!==". Estos operadores no tienen en cuenta la precisión decimal y pueden dar resultados incorrectos al comparar números decimales.

Para evitar este error, es recomendable utilizar comparaciones con una tolerancia decimal. Por ejemplo, se puede definir una función que compare dos números decimales y devuelva verdadero si la diferencia entre ellos es menor que una cierta tolerancia.

Error 3: No considerar la precisión decimal

Un error común es no tener en cuenta la precisión decimal al realizar cálculos con números decimales. Por ejemplo, si se suma "0.1" y "0.2" utilizando el operador de suma "+", es posible obtener un resultado inexacto debido a la representación binaria de los números decimales.

Para evitar este error, es recomendable utilizar una biblioteca o función especializada que maneje números decimales con precisión. Por ejemplo, en lenguajes de programación como Java o C#, se pueden utilizar las clases BigDecimal o Decimal respectivamente para realizar cálculos precisos con números decimales.

Error 4: Comparar cadenas de caracteres en lugar de números

Un error común es comparar cadenas de caracteres en lugar de números decimales. Por ejemplo, si se compara la cadena "0.1" con la cadena "0.01", es posible obtener un resultado incorrecto ya que las cadenas se comparan carácter por carácter y no como números decimales.

Para evitar este error, es recomendable convertir las cadenas de caracteres a números decimales antes de realizar la comparación. Esto se puede hacer utilizando funciones de conversión como "parseFloat()" en JavaScript o "Double.parseDouble()" en Java.

Al comparar números decimales es importante tener en cuenta la precisión decimal y utilizar las herramientas adecuadas para evitar errores comunes. Al utilizar una función de comparación especializada, considerar la tolerancia decimal, utilizar bibliotecas de precisión decimal y convertir las cadenas de caracteres a números decimales, se pueden evitar muchos de los errores comunes al comparar un décimo y un centésimo.

Otras fracciones decimales y cómo se relacionan con un décimo y un centésimo

Las fracciones decimales son aquellas que tienen un numerador y un denominador y se expresan en forma decimal. Son un tipo de fracción especial, ya que su denominador es siempre una potencia de 10. El numerador representa la cantidad de unidades y el denominador representa la posición decimal.

Fracción decimal como un décimo

Una fracción decimal que se puede expresar como un décimo tiene un denominador de 10, lo que significa que el numerador representa una cantidad de unidades de una décima parte. Por ejemplo, la fracción decimal 0.1 se puede expresar como 1/10.

Fracción decimal como un centésimo

Una fracción decimal que se puede expresar como un centésimo tiene un denominador de 100, lo que significa que el numerador representa una cantidad de unidades de una centésima parte. Por ejemplo, la fracción decimal 0.01 se puede expresar como 1/100.

• 0.1 = 1/10
• 0.01 = 1/100
• 0.001 = 1/1000
• 0.0001 = 1/10000

Estas fracciones decimales se encuentran en una posición decimal menor que un número entero y pueden ser expresadas como fracciones de base 10. Son útiles para representar cantidades muy pequeñas, como porcentajes, proporciones y tasas de interés.

Es importante tener en cuenta que las fracciones decimales también se pueden expresar en notación científica, donde el número decimal se escribe como un número entero o un número decimal mayor o igual que 1 multiplicado por una potencia de 10.

Ejemplo de fracción decimal en notación científica:

0.00001 = 1 x 10^-5

Las fracciones decimales se utilizan para representar cantidades pequeñas y se relacionan directamente con un décimo o un centésimo, dependiendo de su posición decimal. Son una forma conveniente de expresar cantidades en situaciones donde los números son muy pequeños y se utilizan con frecuencia en matemáticas, ciencias y economía.

Consejos y trucos para trabajar con fracciones decimales y mejorar la comprensión numérica.

1. Convierte fracciones decimales a fracciones comunes

Si tienes dificultades para trabajar con fracciones decimales, puedes convertirlas a fracciones comunes. Por ejemplo, la fracción decimal 0.5 se convierte en la fracción común 1/2. Esto puede hacer que sea más fácil comprender y trabajar con las fracciones decimales en problemas matemáticos.

2. Utiliza diagramas de barras

Los diagramas de barras son una excelente herramienta para visualizar fracciones decimales. Puedes dibujar una barra dividida en partes iguales para representar una fracción decimal. Por ejemplo, si tienes la fracción decimal 0.75, puedes dibujar una barra dividida en cuatro partes iguales y sombrear tres de esas partes para representar la fracción 3/4.

3. Practica la estimación

La estimación es una habilidad importante cuando se trabaja con fracciones decimales. Puedes practicar estimando el valor de diferentes fracciones decimales para mejorar tu comprensión numérica. Por ejemplo, si tienes la fracción decimal 0.3, puedes estimar que es aproximadamente 1/3.

4. Utiliza modelos manipulativos

Los modelos manipulativos, como fichas o bloques, pueden ser útiles para comprender las fracciones decimales. Puedes usar estos modelos para representar y manipular diferentes fracciones decimales, lo que te ayudará a visualizar su valor y relación con otras fracciones decimales.

5. Practica la comparación de fracciones decimales

Para mejorar tu comprensión numérica con fracciones decimales, es importante practicar la comparación de diferentes fracciones decimales. Puedes hacer esto utilizando símbolos de comparación, como "<", ">" o "=" para determinar si una fracción decimal es mayor, menor o igual a otra fracción decimal.

6. Realiza ejercicios de conversión entre fracciones decimales y porcentajes

Las fracciones decimales y los porcentajes están estrechamente relacionados. Practicar la conversión entre fracciones decimales y porcentajes puede ayudarte a comprender mejor ambos conceptos y mejorar tu comprensión numérica. Por ejemplo, puedes convertir la fracción decimal 0.4 a un porcentaje multiplicándola por 100, lo que resulta en un 40%.

7. Utiliza calculadoras y herramientas en línea

Si tienes dificultades para trabajar con fracciones decimales, puedes utilizar calculadoras y herramientas en línea para realizar cálculos y obtener respuestas precisas. Estas herramientas pueden ser especialmente útiles para realizar operaciones más complejas con fracciones decimales.

Preguntas frecuentes

¿Cuál es más grande, un décimo o un centésimo?

Un décimo es más grande que un centésimo.