Descubre cuánto mide un ángulo casi recto y sorpréndete con nuestras reveladoras cifras

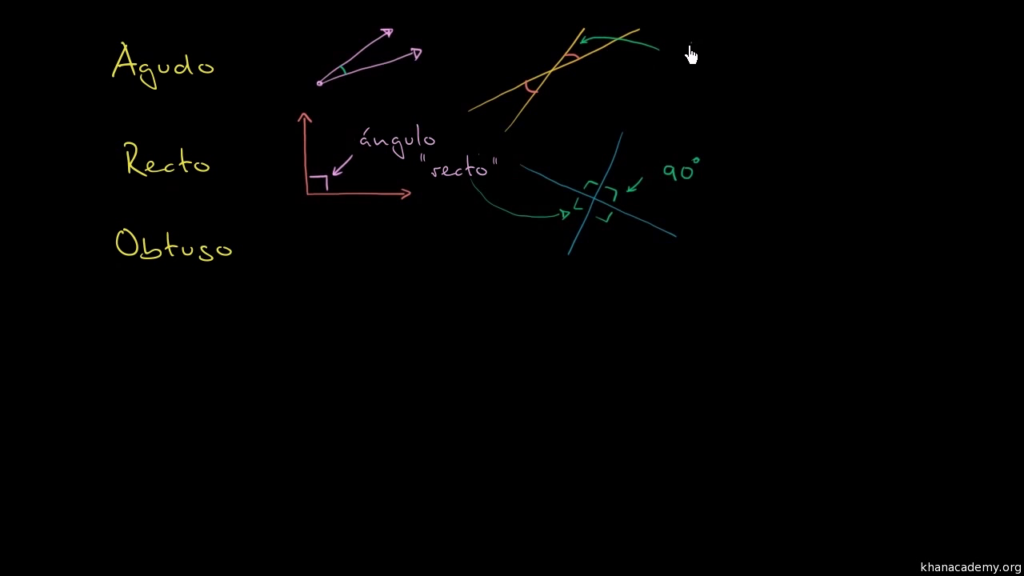
Cuando hablamos de ángulos, generalmente pensamos en ángulos agudos, obtusos o rectos. Sin embargo, existe un tipo de ángulo que se encuentra justo en el límite de ser considerado recto, pero que tiene una medida ligeramente menor. Estamos hablando del ángulo casi recto, que despierta la curiosidad y la intriga en muchos estudiantes y amantes de la geometría.

Vamos a explorar qué es un ángulo casi recto y cuánto mide en comparación con un ángulo recto estándar. Veremos ejemplos prácticos y analizaremos cómo se utiliza esta medida en diferentes áreas del conocimiento. Además, también discutiremos algunos conceptos relacionados, como los ángulos agudos y los ángulos obtusos, para tener una comprensión más completa del tema. Así que prepárate para descubrir los secretos de los ángulos casi rectos y sorprenderte con nuestras reveladoras cifras.

¿Qué es un ángulo casi recto y cómo se diferencia de un ángulo recto?

Un ángulo casi recto es aquel que se acerca mucho a ser un ángulo recto, pero no lo es completamente. Un ángulo recto mide exactamente 90 grados, mientras que un ángulo casi recto puede tener una medida levemente mayor o menor, pero generalmente se encuentra muy cerca de los 90 grados.

La principal diferencia entre un ángulo casi recto y uno recto es su medida. Mientras que un ángulo recto es exactamente de 90 grados, un ángulo casi recto puede ser ligeramente mayor o menor que esta medida. La diferencia puede ser de unos pocos grados, pero es suficiente para considerarlo casi recto en lugar de recto.

Las medidas típicas de un ángulo casi recto: datos asombrosos que debes conocer.

El ángulo casi recto es aquél que tiene una medida muy cercana a los 90 grados, pero no llega a ser exactamente recto. Es un concepto matemático fascinante que tiene muchas aplicaciones en diversos campos, como la geometría, la física y la arquitectura.

Para comprender mejor qué es un ángulo casi recto, es importante conocer las medidas típicas que suelen asociarse a este tipo de ángulo. A continuación, enumeraremos algunas de las medidas más comunes:

1. 89 grados

El ángulo de 89 grados es uno de los más cercanos al ángulo recto. A simple vista, puede parecer prácticamente recto, pero si lo medimos con precisión, encontraremos una diferencia mínima.

2. 88 grados

El ángulo de 88 grados es otro ejemplo de un ángulo casi recto. Aunque la diferencia con el ángulo recto es aún más notable que en el caso anterior, sigue siendo considerado como un ángulo casi recto debido a su cercanía.

3. 91 grados

Aunque técnicamente se considera un ángulo obtuso, el ángulo de 91 grados es lo suficientemente cercano a los 90 grados como para ser mencionado en esta lista. A menudo se utiliza como referencia para comparar la cercanía de otros ángulos al ángulo recto.

4. 87 grados

El ángulo de 87 grados es otro ejemplar de un ángulo casi recto. Aunque la diferencia con el ángulo recto es aún mayor en comparación con los casos previos, sigue siendo considerado como un ángulo cercano.

5. 92 grados

Finalmente, el ángulo de 92 grados también se considera un ángulo casi recto. Aunque se encuentra más alejado del ángulo recto que los ejemplos anteriores, sigue siendo lo suficientemente cercano como para ser clasificado como casi recto.

Los ángulos casi rectos son aquellos que tienen una medida muy cercana a los 90 grados, pero no llegan a ser exactamente rectos. Estas medidas típicas, como 89 grados, 88 grados, 91 grados, 87 grados y 92 grados, permiten visualizar la cercanía de un ángulo a la rectitud y tienen aplicaciones en diversos campos. Comprender estos conceptos nos ayuda a apreciar la importancia y la belleza de la geometría y las matemáticas en nuestro entorno.

Ejemplos de situaciones reales en las que se encuentran ángulos casi rectos.

A continuación, te presento algunos ejemplos de situaciones reales en las que se encuentran ángulos casi rectos:

1. Construcción de edificios

En la construcción de edificios, uno de los elementos clave son los ángulos rectos. Los arquitectos y los ingenieros utilizan instrumentos de medición precisos para asegurarse de que las esquinas de los edificios tengan ángulos de 90 grados. Esto es fundamental para garantizar la estabilidad y la seguridad de la estructura.

2. Diseño de muebles

En el diseño de muebles, también es común encontrar ángulos casi rectos. Por ejemplo, en estanterías, mesas o armarios, se utilizan ángulos rectos para asegurar que las piezas encajen correctamente y que la estructura sea estable. Los carpinteros y diseñadores de muebles utilizan herramientas de medición precisas para lograr ángulos rectos precisos.

3. Trabajo con circuitos electrónicos

En el campo de la electrónica, los ángulos rectos son esenciales en el diseño y montaje de circuitos. Los componentes electrónicos se conectan a placas de circuito impreso (PCB) utilizando ángulos rectos para garantizar una correcta conexión eléctrica y un flujo de señal adecuado. La precisión en los ángulos es clave para evitar cortocircuitos y garantizar el funcionamiento correcto de los dispositivos electrónicos.

4. Agricultura y jardinería

En la agricultura y la jardinería, los ángulos rectos también juegan un papel importante. Por ejemplo, al cultivar plantas en filas, es necesario asegurarse de que las hileras estén dispuestas en ángulos rectos para optimizar el espacio y facilitar el acceso a las plantas. Además, al construir cercas o vallas en jardines o terrenos agrícolas, los ángulos rectos son esenciales para garantizar la estabilidad y la uniformidad de la estructura.

5. Diseño gráfico y web

En el diseño gráfico y web, los ángulos rectos se utilizan para crear estructuras visuales y diseños armónicos. Por ejemplo, en la maquetación de páginas web o en la creación de composiciones gráficas, los diseñadores utilizan cuadrículas y líneas guía con ángulos rectos para organizar y alinear los elementos de forma ordenada y estética.

6. Topografía y cartografía

En la topografía y la cartografía, los ángulos rectos son fundamentales para medir y representar con precisión la forma de la Tierra y la ubicación de las características geográficas. Los topógrafos utilizan equipos de medición especializados, como teodolitos y estaciones totales, para medir ángulos y distancias con gran precisión para crear mapas y representaciones gráficas de la superficie terrestre.

Estos son solo algunos ejemplos en los que se pueden encontrar ángulos casi rectos en situaciones reales. La medida y el control de ángulos rectos son fundamentales en diversos campos y disciplinas para garantizar la precisión, la estabilidad y la funcionalidad de las estructuras y diseños.

La importancia de los ángulos casi rectos en la arquitectura y el diseño.

Los ángulos casi rectos o ángulos cercanos a los 90 grados son de gran importancia en la arquitectura y el diseño. Estas formas geométricas tienen un impacto significativo en la estética y funcionalidad de los espacios construidos.

Estética

Los ángulos casi rectos aportan un aspecto limpio y ordenado a las estructuras arquitectónicas. La simetría y la regularidad que ofrecen estos ángulos generan una sensación de equilibrio y armonía visual. Además, la precisión de las líneas rectas y los ángulos cercanos a los 90 grados transmiten una sensación de solidez y estabilidad.

En el diseño de interiores, los ángulos casi rectos se utilizan para crear una sensación de organización y pulcritud. Las líneas rectas y los ángulos precisos se ven especialmente en muebles y elementos decorativos modernos y minimalistas. Estos ángulos contribuyen a un ambiente ordenado y minimalista, lo que puede ayudar a crear una sensación de calma y serenidad en los espacios.

Funcionalidad

Además de su impacto estético, los ángulos casi rectos también tienen un papel crucial en la funcionalidad de los espacios arquitectónicos. Estos ángulos se utilizan para definir áreas específicas y delimitar espacios. Por ejemplo, los ángulos rectos se utilizan para dividir habitaciones en diferentes áreas funcionales, como una cocina y un comedor en un plano abierto.

Los ángulos casi rectos también son fundamentales en la construcción de estructuras estables y duraderas. Al utilizar ángulos precisos, los arquitectos y diseñadores pueden garantizar la resistencia y rigidez de los edificios. Los ángulos exactos se utilizan en la construcción de paredes, techos, escaleras y otros elementos arquitectónicos para asegurar su estabilidad y rigidez.

Conclusiones

Los ángulos casi rectos son elementos clave en la arquitectura y el diseño. Tanto desde el punto de vista estético como funcional, estos ángulos desempeñan un papel fundamental en la creación de espacios atractivos, ordenados y funcionales. Los ángulos precisos aportan una sensación de equilibrio y solidez a las estructuras arquitectónicas, además de ser fundamentales para garantizar su resistencia y durabilidad.

¿Cómo se calcula la medida de un ángulo casi recto?

Para calcular la medida de un ángulo casi recto, es necesario utilizar el teorema del seno, que relaciona los lados de un triángulo con los senos de sus ángulos.

Supongamos que tenemos un triángulo con un ángulo casi recto, llamado ángulo A, y los lados adyacentes a este ángulo, llamados a y b.

El teorema del seno establece que:

sen(A) = a/b

Si conocemos el valor de a y b, podemos despejar el valor de A. Para ello, utilizamos la función inversa del seno, también conocida como arcseno.

arcsen(a/b) = A

Para calcular el valor de arcsen(a/b), es necesario utilizar una calculadora científica que tenga esa función.

Por ejemplo, si tenemos un triángulo con lados a=3 y b=4, podemos calcular la medida del ángulo A de la siguiente manera:

sen(A) = 3/4

arcsen(3/4) = A

Utilizando una calculadora científica, obtenemos que arcsen(3/4) es aproximadamente 48.59 grados.

Por lo tanto, la medida del ángulo A es de aproximadamente 48.59 grados.

Es importante tener en cuenta que el teorema del seno solo es aplicable en triángulos, por lo que no se puede utilizar para calcular la medida de ángulos casi rectos en otras figuras geométricas.

Curiosidades matemáticas: los ángulos casi rectos más grandes y más pequeños registrados.

En el fascinante mundo de las matemáticas, existen numerosas curiosidades y fenómenos interesantes que desafían nuestra comprensión de la geometría y los ángulos. Uno de estos fenómenos es la existencia de ángulos casi rectos extremadamente grandes y pequeños.

Los ángulos casi rectos más grandes registrados

En la geometría euclidiana, un ángulo recto mide exactamente 90 grados. Sin embargo, en situaciones reales, es posible encontrar ángulos que se aproximan mucho a esta medida, pero que no llegan a ser exactamente de 90 grados. Estos ángulos casi rectos pueden presentarse en diversos contextos, como en la arquitectura, la geometría de la naturaleza o incluso en mediciones científicas.

Los ángulos casi rectos más grandes registrados hasta la fecha son aquellos que se acercan a los 89 grados y 59 minutos. Para poner esto en perspectiva, un ángulo de 89 grados y 59 minutos es solo una fracción de un grado por debajo de un ángulo recto perfecto. Estos ángulos casi rectos extremadamente grandes son sorprendentes, ya que se cree que no existe un ángulo exactamente recto en el mundo real debido a la naturaleza discreta de la geometría euclidiana.

Los ángulos casi rectos más pequeños registrados

En contraste con los ángulos casi rectos grandes, también existen ángulos casi rectos extremadamente pequeños que se acercan a los 0 grados. Estos ángulos casi rectos pueden surgir en diversas situaciones, como en mediciones de precisión o en la geometría de la microscopía.

Los ángulos casi rectos más pequeños registrados son aquellos que se aproximan a los 0 grados y 1 minuto. Esto significa que son ángulos que están a solo una fracción de un grado por encima de ser considerados completamente rectos. Estos ángulos casi rectos extremadamente pequeños son igualmente fascinantes, ya que desafían nuestra intuición y comprensión de la geometría.

Conclusiones

Los ángulos casi rectos más grandes y más pequeños registrados son un testimonio de la complejidad y la belleza de la matemática en el mundo real. Aunque solo sean aproximaciones de ángulos rectos perfectos, su existencia desafía las reglas y los límites de la geometría euclidiana. Estos ángulos casi rectos extremadamente grandes y pequeños nos invitan a explorar y comprender mejor la naturaleza discreta y continua de las formas geométricas en nuestro mundo.

La relación entre los ángulos casi rectos y otras figuras geométricas.

Los ángulos casi rectos son aquellos que tienen una medida muy cercana a los 90 grados. Aunque no son exactamente rectos, su similitud con los ángulos rectos permite establecer algunas relaciones interesantes con otras figuras geométricas.

Relación con los triángulos

En el caso de los triángulos, los ángulos casi rectos pueden aparecer en diferentes tipos de triángulos. Por ejemplo, en los triángulos rectángulos, el ángulo recto es de 90 grados, pero los ángulos agudos pueden ser muy cercanos a los 90 grados, formando así ángulos casi rectos. Estos ángulos pueden ser útiles para resolver problemas de trigonometría y calcular longitudes de lados.

En los triángulos obtusángulos, donde uno de los ángulos es mayor a 90 grados, también pueden encontrarse ángulos casi rectos. Estos ángulos suelen estar cerca de los 90 grados, pero no llegar a serlo. Estos ángulos pueden ser útiles para determinar la clasificación del triángulo y sus propiedades.

Relación con los cuadriláteros

En el caso de los cuadriláteros, los ángulos casi rectos pueden aparecer en diferentes tipos de figuras. Por ejemplo, en los rectángulos, los cuatro ángulos son rectos. Sin embargo, puede haber variaciones en los ángulos que se acerquen a los 90 grados sin llegar a serlo. Estos ángulos pueden afectar la forma y tamaño del rectángulo.

En los trapecios, los ángulos casi rectos pueden encontrarse en las bases o en los ángulos adyacentes a las bases. Estos ángulos pueden influir en la clasificación y propiedades del trapecio.

Relación con otras figuras

Los ángulos casi rectos también pueden aparecer en otras figuras geométricas, como los polígonos regulares e irregulares. En los polígonos regulares, los ángulos casi rectos no son comunes, ya que la suma de los ángulos interiores es siempre constante. Sin embargo, en los polígonos irregulares, pueden aparecer ángulos casi rectos que afecten la forma y la simetría del polígono.

Los ángulos casi rectos tienen una estrecha relación con otras figuras geométricas, como los triángulos, los cuadriláteros y los polígonos. Estos ángulos pueden influir en las propiedades y características de estas figuras, y son importantes en el estudio y aplicación de la geometría.

Consejos para medir y dibujar ángulos casi rectos con precisión.

A continuación, te proporcionaré algunos consejos útiles para medir y dibujar ángulos casi rectos con precisión.

1. Utiliza una escuadra

Una escuadra es una herramienta fundamental para medir y dibujar ángulos rectos. Asegúrate de que la escuadra esté limpia y en buen estado. Coloca la escuadra sobre la línea base y asegúrate de que el ángulo formado sea de 90 grados.

2. Utiliza un transportador

Un transportador es una herramienta que te permite medir y dibujar ángulos con precisión. Coloca el centro del transportador sobre el vértice del ángulo y alinea el lado base del transportador con la línea base del ángulo. Lee el ángulo formado en el transportador.

3. Utiliza una regla graduada

Una regla graduada te permite medir la longitud de los lados del ángulo. Utiliza la regla para medir la longitud de cada lado del ángulo y asegúrate de que sean iguales para un ángulo casi recto.

4. Utiliza una brújula

Una brújula puede ayudarte a dibujar arcos o círculos que estén relacionados con el ángulo. Utiliza la brújula para dibujar arcos o círculos que intersecten los lados del ángulo y te ayuden a visualizar mejor el ángulo.

5. Utiliza la técnica de bisectriz

Para encontrar la bisectriz de un ángulo casi recto, dibuja dos arcos iguales con el mismo radio en cada lado del ángulo. Luego, une los dos puntos de intersección de los arcos y obtendrás la bisectriz del ángulo.

6. Utiliza papel milimetrado

El uso de papel milimetrado puede ser útil para dibujar y medir ángulos casi rectos con precisión. El papel milimetrado te permite medir con mayor precisión las longitudes de los lados del ángulo y dibujar con mayor exactitud las líneas.

Sigue estos consejos y estarás en el camino correcto para medir y dibujar ángulos casi rectos con precisión. Recuerda practicar y tener paciencia, ya que la precisión en el dibujo de ángulos requiere práctica y habilidad.

Aplicaciones prácticas de los ángulos casi rectos en la vida cotidiana.

Los ángulos casi rectos, también conocidos como ángulos cercanos a los 90 grados, tienen diversas aplicaciones prácticas en nuestra vida cotidiana. A continuación, mencionaré algunas de ellas:

1. Construcción y arquitectura:

En la construcción y arquitectura, los ángulos casi rectos son fundamentales para asegurar la estabilidad y precisión de las estructuras. Por ejemplo, al construir una casa, es necesario asegurarse de que los ángulos de las esquinas sean lo más cercanos a los 90 grados posibles, para evitar problemas de deformación o derrumbes. Además, los ángulos casi rectos son utilizados para realizar mediciones precisas en el trazado de líneas rectas y la instalación de elementos arquitectónicos.

2. Diseño gráfico y web:

En el diseño gráfico y web, los ángulos casi rectos son utilizados para crear composiciones equilibradas y estéticamente agradables. Los diseñadores suelen utilizar ángulos casi rectos para alinear elementos visuales como textos, imágenes o botones, logrando una apariencia más ordenada y profesional. Además, estos ángulos pueden ser empleados para definir secciones o divisiones en el diseño de una página web.

3. Fotografía y video:

En la fotografía y el video, los ángulos casi rectos son utilizados para conseguir encuadres simétricos y equilibrados. Al fotografiar o grabar una escena, los fotógrafos y cineastas buscan ángulos casi rectos para asegurar una composición armónica y atractiva visualmente. Además, los ángulos casi rectos también se utilizan en técnicas de edición y retoque fotográfico para corregir distorsiones o enderezar líneas.

4. Topografía y cartografía:

En el campo de la topografía y la cartografía, los ángulos casi rectos son fundamentales para realizar mediciones precisas y representar gráficamente el terreno en mapas. Los topógrafos utilizan equipos especiales para medir ángulos y distancias, y a partir de estos datos, generan planos y mapas con ángulos casi rectos que representan con precisión la forma y características del terreno.

5. Navegación y orientación:

En la navegación marítima y aérea, los ángulos casi rectos son utilizados para determinar rumbos y trayectorias. Los navegantes y pilotos utilizan instrumentos de navegación que les permiten medir ángulos y determinar la posición y dirección correcta. Además, los ángulos casi rectos también son utilizados en brújulas y mapas para orientarse y trazar rutas de navegación.

Los ángulos casi rectos tienen múltiples aplicaciones en diferentes ámbitos de nuestra vida cotidiana. Desde la construcción y arquitectura, hasta el diseño gráfico y la navegación, estos ángulos nos ayudan a lograr precisión, estabilidad y armonía en nuestras actividades diarias.

Explorando la simetría y la perpendicularidad a través de los ángulos casi rectos.

Los ángulos casi rectos son aquellos que se acercan mucho a un ángulo recto, pero no llegan a serlo completamente. Estos ángulos casi rectos son muy interesantes, ya que nos permiten explorar conceptos como la simetría y la perpendicularidad.

Simetría en los ángulos casi rectos

La simetría es una propiedad geométrica que se refiere a la igualdad de dos figuras respecto de un eje o un punto. En el caso de los ángulos casi rectos, podemos observar que si trazamos una línea que pase por el vértice del ángulo y lo divide en dos partes iguales, estas partes serán simétricas entre sí.

Esta simetría nos permite estudiar la relación entre las dos partes del ángulo casi recto y aplicarla a otros problemas geométricos. Además, también nos ayuda a visualizar conceptos como la bisectriz de un ángulo, que es la línea que divide un ángulo en dos partes iguales.

Perpendicularidad en los ángulos casi rectos

La perpendicularidad es otra propiedad geométrica que se refiere a la formación de un ángulo de 90 grados entre dos líneas o segmentos. En el caso de los ángulos casi rectos, podemos observar que uno de los lados del ángulo casi recto es perpendicular al otro lado.

Esta perpendicularidad nos permite estudiar la relación entre los ángulos casi rectos y las líneas perpendiculares. Por ejemplo, podemos utilizar un ángulo casi recto para construir líneas perpendiculares en la construcción de figuras geométricas.

• Los ángulos casi rectos nos permiten explorar conceptos como la simetría y la perpendicularidad en la geometría.
• La simetría en los ángulos casi rectos nos permite estudiar la relación entre las dos partes del ángulo y aplicarla a otros problemas geométricos.
• La perpendicularidad en los ángulos casi rectos nos ayuda a construir líneas perpendiculares en la construcción de figuras geométricas.

Preguntas frecuentes

1. ¿Qué es un ángulo casi recto?

Un ángulo casi recto es aquel que se acerca mucho a los 90 grados, pero no alcanza a formar un ángulo recto perfecto.

2. ¿Cuánto mide un ángulo casi recto?

Un ángulo casi recto puede medir aproximadamente entre 85 y 89 grados.

3. ¿Cuál es la diferencia entre un ángulo casi recto y un ángulo recto?

La diferencia radica en que un ángulo casi recto se acerca a los 90 grados pero no los alcanza, mientras que un ángulo recto tiene exactamente 90 grados.

4. ¿Dónde se pueden encontrar ángulos casi rectos en la vida cotidiana?

Los ángulos casi rectos se pueden encontrar en muchos objetos y situaciones cotidianas, como en la esquina de una mesa, en el techo de una casa o en la forma de una hoja de papel doblada.

5. ¿Cuál es la importancia de conocer y entender los ángulos casi rectos?

Conocer y entender los ángulos casi rectos nos permite comprender mejor la geometría y aplicarlo en diversas disciplinas como la arquitectura, la ingeniería y la física.