Domina las fracciones equivalentes en primaria 4º grado y mejora tu rendimiento escolar

Las fracciones son un concepto matemático muy importante en la educación primaria. A medida que los niños avanzan en su aprendizaje, deben comprender cómo funcionan las fracciones equivalentes. Esta habilidad les permitirá simplificar fracciones, compararlas y realizar operaciones matemáticas más complejas. Dominar las fracciones equivalentes es fundamental para el éxito académico en matemáticas.

Exploraremos qué son las fracciones equivalentes y por qué son importantes en el currículo de matemáticas de 4º grado. También veremos cómo encontrar fracciones equivalentes utilizando diferentes métodos y actividades que puedes hacer para ayudar a tus hijos a comprender y practicar este concepto. Con la práctica constante, los estudiantes podrán mejorar su rendimiento escolar y tener un mejor dominio de las fracciones en general.

Introducción a las fracciones equivalentes

Las fracciones equivalentes son aquellas que representan la misma cantidad, pero tienen diferentes numeradores y denominadores. En otras palabras, son fracciones que se pueden simplificar o amplificar para obtener una fracción diferente con el mismo valor.

Para entender cómo funcionan las fracciones equivalentes, es importante recordar que una fracción está compuesta por dos partes: el numerador y el denominador. El numerador representa la cantidad de partes que se toman de un todo, mientras que el denominador representa el total de partes en el todo.

Para demostrar que dos fracciones son equivalentes, se multiplican o dividen tanto el numerador como el denominador por el mismo número. De esta manera, se puede obtener una fracción diferente con el mismo valor que la fracción original.

Ejemplo de fracciones equivalentes

Supongamos que tenemos la fracción 3/6. Si multiplicamos tanto el numerador como el denominador por 2, obtenemos la fracción equivalente 6/12. Ambas fracciones representan la misma cantidad, es decir, la mitad de un todo.

También es posible simplificar una fracción para encontrar su equivalente. Por ejemplo, si tenemos la fracción 8/16, podemos dividir tanto el numerador como el denominador por 8 y obtenemos la fracción equivalente 1/2. Ambas fracciones representan la mitad de un todo.

Propiedad de las fracciones equivalentes

Una propiedad importante de las fracciones equivalentes es que se pueden utilizar para comparar y ordenar fracciones. Al tener el mismo valor, las fracciones equivalentes pueden ser utilizadas para determinar si una fracción es mayor o menor que otra.

Por ejemplo, si queremos comparar las fracciones 1/3 y 2/6, podemos encontrar que son equivalentes ya que ambos representan un tercio de un todo. Por lo tanto, podemos concluir que ambas fracciones son iguales.

Las fracciones equivalentes son aquellas que representan la misma cantidad, pero tienen diferentes numeradores y denominadores. Se pueden obtener fracciones equivalentes multiplicando o dividiendo tanto el numerador como el denominador por el mismo número. Estas fracciones son útiles para comparar y ordenar fracciones, ya que tienen el mismo valor.

¿Qué son las fracciones equivalentes?

Las fracciones equivalentes son fracciones que representan la misma cantidad, pero están escritas de forma diferente. En otras palabras, son fracciones que tienen diferentes numeradores y denominadores, pero cuando se simplifican, dan el mismo resultado.

Para entender mejor el concepto de fracciones equivalentes, es importante recordar que una fracción se compone de dos partes: el numerador y el denominador. El numerador indica la cantidad de partes que se toman o se tienen, mientras que el denominador indica en cuántas partes se divide un todo.

Para determinar si dos fracciones son equivalentes, se puede hacer uso de la simplificación. Simplificar una fracción implica dividir tanto el numerador como el denominador por su máximo común divisor (MCD). Si el resultado de la simplificación de ambas fracciones es el mismo, entonces se consideran equivalentes.

Por ejemplo, consideremos las fracciones 2/4 y 1/2. Para simplificar la fracción 2/4, dividimos el numerador y el denominador por su MCD, que en este caso es 2. Por lo tanto, 2/4 se simplifica a 1/2, que es la misma fracción que 1/2. Por lo tanto, estas dos fracciones son equivalentes.

Las fracciones equivalentes son útiles en diversos contextos matemáticos, ya que permiten representar la misma cantidad de diferentes maneras. Por ejemplo, en un problema de reparto de alimentos, se puede expresar la cantidad que recibe cada persona en forma de fracción. Si dos fracciones son equivalentes, esto significa que la cantidad que recibe cada persona es la misma, independientemente de cómo se expresen las fracciones.

Las fracciones equivalentes son fracciones que representan la misma cantidad, pero están escritas de forma diferente. Se pueden determinar mediante la simplificación de las fracciones y son útiles en diversos contextos matemáticos.

Importancia de las fracciones equivalentes en matemáticas

Las fracciones equivalentes son un concepto fundamental en matemáticas y juegan un papel clave en el aprendizaje y la resolución de problemas relacionados con fracciones. Una fracción equivalente es aquella que representa la misma cantidad que otra fracción, pero que tiene diferente forma o expresión decimal.

La importancia de las fracciones equivalentes radica en su utilidad para simplificar y comparar fracciones, así como para realizar operaciones aritméticas con ellas. Al poder transformar una fracción en una equivalente más simple, facilita el cálculo y la comprensión de los conceptos matemáticos.

Simplificación de fracciones

Una de las principales aplicaciones de las fracciones equivalentes es la simplificación de fracciones. Al encontrar una fracción equivalente en la que el numerador y el denominador sean divisibles por el mismo número, se puede reducir la fracción a su forma más simple.

Por ejemplo, si tenemos la fracción 6/12, podemos encontrar una fracción equivalente dividiendo tanto el numerador como el denominador por 6. Esto nos daría la fracción simplificada 1/2, que representa la misma cantidad pero en una forma más simple.

Comparación de fracciones

Otra aplicación importante de las fracciones equivalentes es la comparación de fracciones. Al encontrar una fracción equivalente para cada una de las fracciones que se desea comparar, se puede determinar cuál es mayor o menor.

Por ejemplo, si queremos comparar las fracciones 3/4 y 2/3, podemos encontrar fracciones equivalentes en las que ambos denominadores sean iguales. En este caso, podemos encontrar fracciones equivalentes multiplicando el numerador y el denominador de cada fracción por el denominador de la otra fracción.

Al encontrar fracciones equivalentes, en este caso, obtendríamos las fracciones 9/12 y 8/12. Como el denominador es el mismo, podemos comparar los numeradores para determinar que 9/12 es mayor que 8/12.

Operaciones aritméticas con fracciones

Las fracciones equivalentes también son útiles para realizar operaciones aritméticas con fracciones. Al tener fracciones con denominadores diferentes, es necesario encontrar fracciones equivalentes con el mismo denominador antes de realizar la operación.

Por ejemplo, si queremos sumar las fracciones 1/2 y 1/4, primero debemos encontrar fracciones equivalentes con el mismo denominador. En este caso, podemos multiplicar el numerador y el denominador de la primera fracción por 2, y el numerador y el denominador de la segunda fracción por 4.

Al encontrar fracciones equivalentes, obtendríamos las fracciones 2/4 y 1/4. Luego, podemos sumar las dos fracciones equivalentes para obtener el resultado final: 3/4.

Las fracciones equivalentes son fundamentales en matemáticas para simplificar, comparar y realizar operaciones aritméticas con fracciones. Su comprensión y aplicación correcta permiten resolver problemas de manera más eficiente y precisa.

Cómo identificar fracciones equivalentes

Cuando trabajamos con fracciones, es común encontrarnos con fracciones equivalentes. Esto significa que representan la misma cantidad, pero están escritas de forma diferente.

Identificar fracciones equivalentes es una habilidad importante en matemáticas, ya que nos permite simplificar las fracciones y realizar operaciones de manera más sencilla.

¿Qué es una fracción equivalente?

Una fracción es equivalente a otra cuando representan la misma cantidad, pero están escritas de forma diferente. Esto significa que el numerador y el denominador de ambas fracciones son múltiplos o divisibles entre sí.

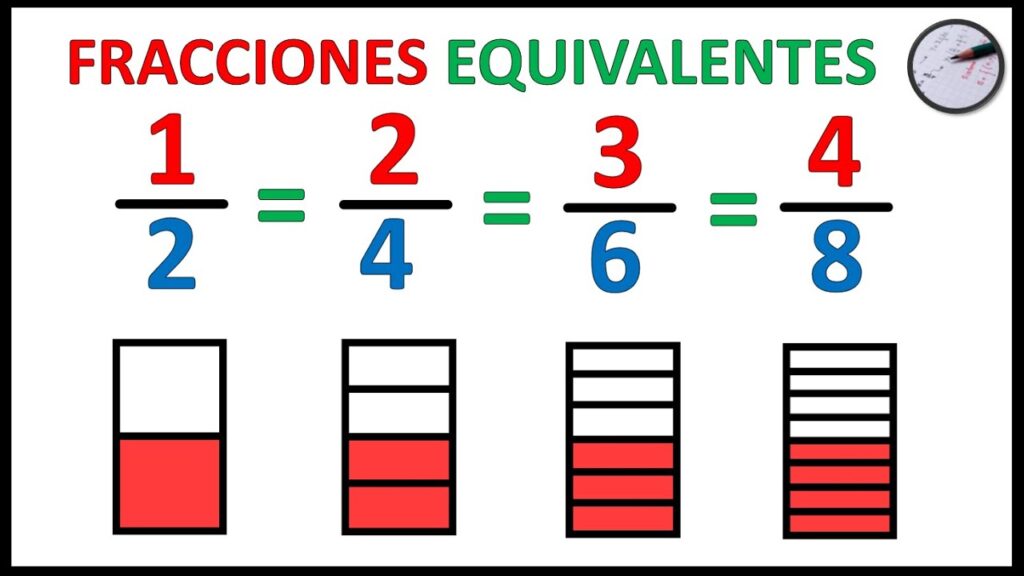
Por ejemplo, las fracciones 1/2, 2/4 y 3/6 son equivalentes, ya que todas representan la mitad de una cantidad.

Cómo identificar fracciones equivalentes

Existen diferentes métodos para identificar fracciones equivalentes. A continuación, te mostraré algunos de los más comunes:

• Método de simplificación: Para identificar fracciones equivalentes, podemos simplificar las fracciones reduciendo el numerador y el denominador a su forma más simple. Por ejemplo, la fracción 4/8 se puede simplificar a 1/2 dividiendo ambos números por el mismo factor común, en este caso, el 4.
• Método de multiplicación: Otra forma de identificar fracciones equivalentes es multiplicando o dividiendo el numerador y el denominador de una fracción por el mismo número. Por ejemplo, la fracción 2/3 es equivalente a 4/6 ya que multiplicamos el numerador y el denominador por 2.
• Método de comparación: También podemos identificar fracciones equivalentes comparándolas entre sí. Si dos fracciones tienen el mismo valor decimal o representan la misma parte de un todo, entonces son equivalentes. Por ejemplo, las fracciones 1/4 y 25/100 son equivalentes, ya que ambas representan el 25% de una cantidad.

Ejemplos de fracciones equivalentes

A continuación, te mostraré algunos ejemplos de fracciones equivalentes:

1. 1/2 es equivalente a 2/4 y 3/6.
2. 2/3 es equivalente a 4/6.
3. 3/4 es equivalente a 6/8 y 9/12.
4. 5/8 es equivalente a 10/16.

Recuerda que para identificar fracciones equivalentes, debes simplificar o comparar las fracciones para determinar si representan la misma cantidad.

Estrategias para encontrar fracciones equivalentes

En matemáticas, las fracciones equivalentes son aquellas que representan la misma cantidad, pero tienen diferentes numeradores y denominadores. En otras palabras, son fracciones que tienen el mismo valor, pero están escritas de manera diferente.

Encontrar fracciones equivalentes puede ser útil en diversas situaciones, como simplificar una fracción, comparar fracciones o resolver problemas matemáticos. A continuación, te presento algunas estrategias para encontrar fracciones equivalentes:

Multiplicar o dividir el numerador y el denominador por el mismo número

Una estrategia común para encontrar fracciones equivalentes es multiplicar o dividir tanto el numerador como el denominador de la fracción original por el mismo número. Al hacer esto, mantendrás el mismo cociente y, por lo tanto, no alterarás el valor de la fracción original.

Por ejemplo, si tienes la fracción 2/3, puedes multiplicar tanto el numerador como el denominador por 2, obteniendo así la fracción equivalente 4/6. De manera similar, puedes dividir ambos por 3, lo que resultará en la fracción equivalente 2/3.

Utilizar la propiedad de fracciones equivalentes

Otra forma de encontrar fracciones equivalentes es utilizando la propiedad de fracciones equivalentes. Esta propiedad establece que si multiplicamos o dividimos el numerador y el denominador de una fracción por el mismo número distinto de cero, obtendremos una fracción equivalente.

Por ejemplo, si tienes la fracción 1/2, puedes multiplicar tanto el numerador como el denominador por 2/2, obteniendo así la fracción equivalente 2/4. Del mismo modo, puedes multiplicar ambos por 3/3, lo que resultará en la fracción equivalente 3/6.

Usar el mcm (mínimo común múltiplo)

Una tercera estrategia para encontrar fracciones equivalentes es utilizar el mcm (mínimo común múltiplo) de los denominadores. El mcm es el número más pequeño que es múltiplo común de dos o más números y se utiliza para encontrar un denominador común en fracciones con diferentes denominadores.

Por ejemplo, si tienes las fracciones 3/4 y 2/5, el mcm de 4 y 5 es 20. Por lo tanto, puedes multiplicar el numerador y el denominador de la primera fracción por 5/5 y la segunda fracción por 4/4, obteniendo las fracciones equivalentes 15/20 y 8/20, respectivamente.

Estas son algunas estrategias que puedes utilizar para encontrar fracciones equivalentes. Recuerda que es importante practicar y familiarizarse con ellas para poder aplicarlas en diferentes problemas y situaciones matemáticas.

Uso de diagramas de fracciones para visualizar las fracciones equivalentes

Los diagramas de fracciones son una herramienta visual muy útil para comprender y visualizar las fracciones equivalentes. Estos diagramas se utilizan para representar las fracciones mediante círculos divididos en partes iguales.

Creación de un diagrama de fracciones

Para crear un diagrama de fracciones, se dibuja un círculo y se divide en el número de partes iguales que representa el denominador de la fracción. Por ejemplo, si tenemos la fracción 3/4, se dibuja un círculo y se divide en 4 partes iguales.

Luego, se colorea el número de partes que representa el numerador de la fracción. En el caso de la fracción 3/4, se colorean 3 de las 4 partes del círculo. De esta manera, se representa visualmente la fracción.

Visualización de fracciones equivalentes

Una vez creado el diagrama de fracciones, podemos utilizarlo para visualizar las fracciones equivalentes.

Por ejemplo, si tenemos la fracción 2/8, se dibuja un círculo y se divide en 8 partes iguales. Luego, se colorean 2 de las 8 partes del círculo. Al comparar este diagrama con el de la fracción 3/4, podemos ver que ambas fracciones representan la misma cantidad, ya que los diagramas son iguales.

Beneficios de los diagramas de fracciones

Los diagramas de fracciones son una herramienta educativa muy útil, especialmente para los estudiantes que tienen dificultades para comprender las fracciones.

Estos diagramas permiten visualizar de manera clara y concreta las fracciones y sus equivalencias, lo que facilita su comprensión y manipulación.

Además, los diagramas de fracciones también son útiles para comparar fracciones y realizar operaciones matemáticas, como sumas y restas de fracciones.

Conclusión

Los diagramas de fracciones son una herramienta visual muy útil para comprender y visualizar las fracciones equivalentes. Estos diagramas permiten representar las fracciones de forma clara y concreta, facilitando su comprensión y manipulación.

Si tienes dificultades para entender las fracciones, te recomiendo utilizar los diagramas de fracciones como una forma de aprender y practicar este concepto matemático de manera más visual y sencilla.

Ejemplos prácticos de fracciones equivalentes en problemas matemáticos

Las fracciones equivalentes son aquellas que representan la misma cantidad, pero que tienen diferentes numeradores y denominadores. En matemáticas, es común trabajar con fracciones equivalentes para simplificar cálculos y resolver problemas de manera más fácil.

A continuación, se presentarán algunos ejemplos prácticos de fracciones equivalentes en problemas matemáticos:

Ejemplo 1: Repartir pizza

Imagina que tienes una pizza entera y quieres compartirla con tus amigos. Si la pizza se divide en 8 pedazos y tienes 5 amigos, ¿qué fracción de la pizza le corresponde a cada uno?

Para resolver este problema, podemos encontrar la fracción equivalente que represente la porción de la pizza que corresponde a cada amigo. Si dividimos la pizza en 8 pedazos y tenemos 5 amigos, cada amigo obtendrá ¹/₈ de la pizza. Para encontrar una fracción equivalente, podemos multiplicar tanto el numerador como el denominador por el mismo número. Por ejemplo, si multiplicamos tanto el numerador como el denominador de ¹/₈ por 2, obtenemos ²/₁₆. Entonces, cada amigo obtendrá ²/₁₆ de la pizza.

Ejemplo 2: Comparar fracciones

Supongamos que queremos comparar las fracciones ²/₃ y ³/₄ para determinar cuál es mayor.

Para hacer esta comparación, podemos encontrar fracciones equivalentes con el mismo denominador. Si multiplicamos tanto el numerador como el denominador de ²/₃ por 4, obtenemos ⁸/₁₂. Si multiplicamos tanto el numerador como el denominador de ³/₄ por 3, obtenemos ⁹/₁₂. Ahora, podemos comparar las fracciones ⁸/₁₂ y ⁹/₁₂. Al tener el mismo denominador, podemos comparar los numeradores y determinar que ⁹/₁₂ es mayor que ⁸/₁₂.

Ejemplo 3: Expresión decimal como fracción

Imaginemos que tenemos la expresión decimal 0.75 y queremos escribirla como fracción.

Podemos considerar que el número decimal tiene dos lugares decimales, por lo que podemos expresarlo como ⁷⁵/₁₀₀. Sin embargo, también podemos simplificar esta fracción encontrando una fracción equivalente. Si dividimos tanto el numerador como el denominador de ⁷⁵/₁₀₀ por 25, obtendremos la fracción simplificada ³/₄. Por lo tanto, la expresión decimal 0.75 se puede escribir como la fracción ³/₄.

Estos ejemplos demuestran cómo utilizar fracciones equivalentes en problemas matemáticos para simplificar cálculos y obtener resultados más precisos. Es importante entender el concepto de fracciones equivalentes y cómo se pueden aplicar en diferentes contextos para resolver problemas matemáticos de manera más eficiente.

Cómo simplificar fracciones para encontrar fracciones equivalentes

Una fracción se considera simplificada cuando el numerador y el denominador no tienen factores comunes además del 1. Sin embargo, a veces es necesario simplificar una fracción para encontrar fracciones equivalentes.

Pasos para simplificar una fracción:

1. Identificar los factores primos del numerador y el denominador.
2. Eliminar los factores comunes tanto del numerador como del denominador.
3. Escribir la fracción resultante con los factores restantes.

Ejemplo:

Supongamos que queremos simplificar la fracción 12/24.

1. Los factores primos de 12 son 2, 2 y 3.
2. Los factores primos de 24 son 2, 2, 2 y 3.
3. Eliminamos los factores comunes del numerador y el denominador. En este caso, eliminamos un 2 y un 3.
4. La fracción simplificada es 1/2.

Es importante recordar que cualquier fracción puede ser simplificada. En algunos casos, es posible simplificar fracciones de manera más compleja utilizando técnicas adicionales, pero el método mencionado anteriormente es el más común y sencillo de utilizar.

Cómo comparar fracciones equivalentes

Comparar fracciones equivalentes es un proceso sencillo que nos permite determinar si dos fracciones representan la misma cantidad. Para hacerlo, debemos seguir los siguientes pasos:

Paso 1: Encontrar una fracción equivalente

El primer paso consiste en encontrar una fracción equivalente para cada una de las fracciones que queremos comparar. Para ello, debemos multiplicar o dividir el numerador y el denominador de la fracción original por el mismo número.

Por ejemplo, si queremos comparar las fracciones 2/4 y 1/2, podemos encontrar una fracción equivalente para la primera multiplicando tanto el numerador como el denominador por 2, quedando así: 4/8. Para la segunda fracción, no es necesario hacer ningún cambio ya que ya está en su forma más simple.

Paso 2: Comparar las fracciones

Una vez que tenemos las fracciones equivalentes, podemos compararlas fácilmente. Para ello, debemos fijarnos en el numerador de cada fracción y determinar cuál es mayor. Si los numeradores son iguales, entonces las fracciones son equivalentes.

Ejemplo:

Tomemos las fracciones 3/6 y 2/4 como ejemplo:

• Encontramos una fracción equivalente para la primera multiplicando numerador y denominador por 2, resultando en 6/12.
• La segunda fracción ya está en su forma más simple.
• Al comparar los numeradores, vemos que 6 es mayor que 2.

Por lo tanto, podemos concluir que 3/6 es mayor que 2/4.

Aplicaciones de las fracciones equivalentes en la vida diaria

Las fracciones equivalentes son una herramienta matemática que nos permite representar la misma cantidad de una manera diferente. Esto tiene diversas aplicaciones en la vida diaria, tanto en situaciones cotidianas como en campos más especializados.

1. Cocina y repostería

En la cocina y la repostería, las fracciones equivalentes son muy útiles para ajustar las cantidades de ingredientes en una receta. Si necesitamos una cantidad más pequeña o más grande de un ingrediente, podemos utilizar fracciones equivalentes para lograrlo sin modificar la proporción de la receta original.

Por ejemplo, si una receta requiere media taza de azúcar y queremos hacer la mitad de la receta, podemos utilizar una fracción equivalente al dividir la media taza entre 2, obteniendo un cuarto de taza de azúcar.

2. Compras y descuentos

Las fracciones equivalentes también nos ayudan a comparar precios y calcular descuentos. Por ejemplo, si un producto tiene un descuento del 20%, podemos encontrar el precio rebajado multiplicando el precio original por la fracción equivalente a 0.8.

De esta forma, las fracciones equivalentes nos permiten determinar rápidamente el precio final y realizar comparaciones entre diferentes opciones de compra.

3. Escalas y planos

En la arquitectura y el diseño, las fracciones equivalentes se utilizan para representar escalas en planos y maquetas. Esto permite reducir o ampliar las dimensiones de un objeto o espacio para representarlo de manera adecuada en un plano.

Por ejemplo, si queremos representar una casa en un plano escala 1:50, podemos utilizar una fracción equivalente como 1/50 para representar las dimensiones reales de la casa en el plano.

4. Finanzas personales

Las fracciones equivalentes también son útiles en finanzas personales, especialmente al calcular porcentajes y tasas de interés. Al utilizar fracciones equivalentes, podemos determinar rápidamente cuánto dinero ganaremos o pagaremos en concepto de intereses.

Por ejemplo, si tomamos un préstamo con una tasa de interés del 10%, podemos utilizar una fracción equivalente como 0.1 para calcular cuánto pagaremos en intereses por cada unidad de dinero prestado.

Las fracciones equivalentes tienen diversas aplicaciones en la vida diaria, desde la cocina hasta las finanzas personales. Nos permiten ajustar cantidades, calcular descuentos, representar escalas y calcular tasas de interés, entre otras cosas. Dominar este concepto matemático nos brinda una herramienta valiosa para resolver problemas y tomar decisiones de manera más eficiente.

Ejercicios y actividades para practicar fracciones equivalentes en el aula

Las fracciones equivalentes son un tema importante en las matemáticas, ya que permiten representar la misma cantidad de manera diferente. En el aula, es fundamental que los estudiantes practiquen y refuercen este concepto para fortalecer su comprensión y habilidades matemáticas.

1. Juego de cartas

Una actividad divertida y práctica es el juego de cartas de fracciones equivalentes. Para realizar este juego, cada estudiante debe tener un mazo de cartas con fracciones escritas en ellas. El objetivo del juego es encontrar fracciones equivalentes en el mazo y formar parejas. El estudiante que logre formar la mayor cantidad de parejas gana el juego.

2. Tablero de fracciones

En este ejercicio, el docente puede crear un tablero con diferentes fracciones escritas en él. Cada estudiante recibirá una ficha con una fracción y deberá colocarla en el lugar correspondiente en el tablero. Los estudiantes deben buscar la fracción equivalente en el tablero y colocar su ficha en ese lugar. Al finalizar, se puede verificar si los estudiantes han colocado las fichas correctamente.

3. Actividad de recorte y pegado

En esta actividad, los estudiantes pueden recortar diferentes formas geométricas y dividirlas en diferentes partes. Luego, deben pegar las partes en un papel y escribir la fracción correspondiente a cada parte. Los estudiantes deben encontrar fracciones equivalentes y agrupar las partes que representen la misma cantidad.

4. Juego de bingo de fracciones

El juego de bingo de fracciones es una forma divertida de practicar fracciones equivalentes en el aula. El docente puede crear diferentes tarjetas de bingo con fracciones escritas en ellas. Los estudiantes deben marcar las fracciones equivalentes en su tarjeta a medida que se van anunciando. El estudiante que complete su tarjeta primero, gana el juego.

5. Actividad de comparación de fracciones

En esta actividad, los estudiantes deben comparar diferentes pares de fracciones y determinar si son equivalentes o no. Pueden utilizar manipulativos como bloques o fichas para visualizar y comparar las fracciones. Los estudiantes deben justificar su respuesta y explicar por qué las fracciones son o no equivalentes.

Estas son solo algunas ideas de ejercicios y actividades que pueden ser utilizadas para practicar fracciones equivalentes en el aula. Es importante adaptar las actividades al nivel y las necesidades de los estudiantes, fomentando el trabajo en equipo y la participación activa.

Recursos en línea para reforzar el aprendizaje de fracciones equivalentes

Las fracciones equivalentes son un tema importante en matemáticas y comprender cómo trabajar con ellas puede ser un desafío para muchos estudiantes. Afortunadamente, hay una serie de recursos en línea que pueden ayudar a reforzar el aprendizaje de fracciones equivalentes de una manera divertida y interactiva.

1. Khan Academy

Khan Academy es una plataforma en línea que ofrece una amplia gama de lecciones y ejercicios gratuitos sobre diversos temas matemáticos. En su sección de fracciones, puedes encontrar lecciones que explican de manera clara y sencilla cómo trabajar con fracciones equivalentes. Además, ofrece una gran cantidad de ejercicios prácticos para que los estudiantes practiquen y refuercen sus habilidades.

2. Math Playground

Math Playground es otro recurso en línea fantástico que ofrece una variedad de juegos interactivos para que los estudiantes practiquen fracciones equivalentes. Los juegos están diseñados de forma divertida y desafiante, lo que los hace ideales para motivar a los estudiantes a practicar y aprender más sobre este tema. Además, Math Playground también ofrece videos instructivos y problemas de práctica adicionales.

3. Math is Fun

Math is Fun es un sitio web que busca hacer que las matemáticas sean más divertidas y accesibles para los estudiantes. En su sección de fracciones, ofrece explicaciones claras y concisas sobre cómo trabajar con fracciones equivalentes, junto con ejemplos y ejercicios prácticos. También incluye una calculadora de fracciones en línea que puede ser útil para verificar los cálculos.

4. Prodigy

Prodigy es un juego en línea basado en la matemática que permite a los estudiantes practicar una variedad de conceptos matemáticos, incluyendo fracciones equivalentes. Con una interfaz de juego cautivadora y recompensas por completar tareas y desafíos, Prodigy puede ser una excelente manera de motivar a los estudiantes a aprender y practicar fracciones equivalentes de una manera divertida y atractiva.

5. YouTube

YouTube es una fuente inagotable de videos educativos sobre matemáticas y otros temas. Buscar "fracciones equivalentes" en YouTube te dará acceso a una amplia variedad de videos instructivos que explican el concepto paso a paso. Los estudiantes pueden seguir estos videos a su propio ritmo, pausar y repetir cuando sea necesario, y aprender de manera interactiva.

Utilizar recursos en línea para reforzar el aprendizaje de fracciones equivalentes puede ser una excelente manera de complementar las lecciones en el aula y ayudar a los estudiantes a comprender este tema de manera más efectiva. Estos recursos ofrecen una variedad de enfoques y actividades, lo que permite a los estudiantes aprender de acuerdo a su propio ritmo y estilo de aprendizaje. ¡Así que no dudes en explorar estos recursos y dar un impulso a tu comprensión de fracciones equivalentes!

Conclusiones y consejos finales para dominar las fracciones equivalentes en primaria 4º grado.

Las fracciones equivalentes son una parte fundamental del aprendizaje matemático en cuarto grado de primaria. A través de la comprensión de este concepto, los estudiantes pueden desarrollar habilidades de razonamiento matemático y aplicarlas en situaciones de la vida real.

Para dominar las fracciones equivalentes, es importante tener en cuenta algunos consejos y recomendaciones:

1. Comprender qué son las fracciones equivalentes:

Antes de empezar a trabajar con fracciones equivalentes, es necesario entender qué son y cómo se forman. Las fracciones equivalentes son aquellas que representan la misma cantidad, pero que están escritas de forma distinta. Por ejemplo, 1/2 y 2/4 son fracciones equivalentes porque representan la misma cantidad de una unidad.

2. Identificar patrones:

Una vez que se comprende qué son las fracciones equivalentes, es importante buscar patrones y reglas que permitan identificar cuándo dos fracciones son equivalentes. Por ejemplo, si se multiplican o dividen el numerador y el denominador de una fracción por el mismo número, se obtendrá una fracción equivalente. Este conocimiento puede facilitar la identificación de fracciones equivalentes en diferentes contextos.

3. Utilizar estrategias visuales:

Las estrategias visuales, como los diagramas de fracciones y los modelos manipulativos, son herramientas útiles para comprender y analizar las fracciones equivalentes. Estas representaciones visuales pueden ayudar a los estudiantes a visualizar la relación entre diferentes fracciones y a encontrar fracciones equivalentes de manera más fácil.

4. Practicar con ejercicios y problemas:

La práctica constante es clave para dominar las fracciones equivalentes. Es recomendable resolver una variedad de ejercicios y problemas que involucren fracciones equivalentes, tanto en el aula como en casa. Esto permitirá a los estudiantes fortalecer sus habilidades y aplicar los conceptos aprendidos en situaciones reales.

5. Aplicar las fracciones equivalentes en la vida diaria:

Es importante destacar la relevancia de las fracciones equivalentes en situaciones cotidianas. Animar a los estudiantes a identificar ejemplos de fracciones equivalentes en su entorno puede ayudarles a comprender mejor la utilidad y la aplicabilidad de este concepto en la vida diaria.

Dominar las fracciones equivalentes en cuarto grado de primaria requiere comprensión, práctica y aplicación en situaciones reales. Siguiendo estos consejos y recomendaciones, los estudiantes pueden fortalecer sus habilidades matemáticas y desarrollar una base sólida para el aprendizaje futuro.

Preguntas frecuentes

¿Qué son las fracciones equivalentes?

Las fracciones equivalentes son aquellas que representan la misma cantidad, pero tienen diferentes numeradores y denominadores.

¿Cómo se pueden encontrar fracciones equivalentes?

Para encontrar fracciones equivalentes, se puede multiplicar o dividir tanto el numerador como el denominador por el mismo número.

¿Por qué es importante dominar las fracciones equivalentes?

Es importante dominar las fracciones equivalentes porque nos permite simplificar y comparar fracciones, así como resolver problemas matemáticos de manera más eficiente.

¿Cómo se pueden simplificar las fracciones equivalentes?

Las fracciones se pueden simplificar dividiendo tanto el numerador como el denominador por su máximo común divisor.

¿Cómo se pueden comparar fracciones equivalentes?

Las fracciones equivalentes se pueden comparar al obtener un denominador común y luego comparar los numeradores.